Wie geht das?

Answer 1

[merkurus]

Aufgabe 18
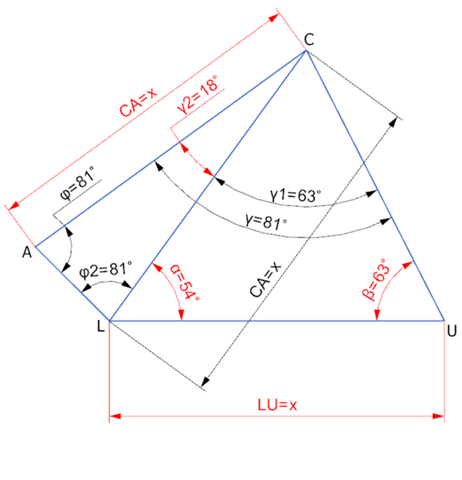
Die Winkelsumme in einem Dreieck beträgt 180°
Also können wir rechnen für γ1 (Rechtes Dreieck)
γ1 = 180 - α - β
γ1 = 180 - 54 - 63
γ1 = 63°
---
Da β und γ1 jeweils 63° betragen ist es
ein gleichschenkliges Dreieck
Somit ist CL genauso groß wie LU und CA.
---
Da auch das linke Dreieck gleichschenklig ist
CL und CA haben die gleiche Länge
Können wir rechnen für Winkel φ
φ = (180 - γ2) / 2
φ = (180 - 18) / 2
φ = 81°

Answer 2

[gauss58]

Winkel LCU = 180° - 54° - 63° = 63°

Folglich ist Dreieck LUC gleichschenklig und damit LU = LC.

Lt. Vorgabe ist LU = CA, also ist CA = LC. Damit ist Dreieck ALC auch gleichschenklig.

φ = (180° - 18°) / 2 = 81°