Wie berechne ich das zeichnerisch/rechnerisch?
Die Aufgabe: Während ein Krankenwagen mit einem Verletzen, aber OHNE Arzt, in Richtung des 30km entfernten Krankenhauses startet, fährt gleichzeitig vom Krankenhaus ein Notarzt los, dem Krankenwagen entgegen. Dessen mittlere Geschwindigkeit beträgt 60 km/h, die des Notarztes 90 km/h. Bestimme, wie viele Minuten nach dem Losfahren der Verletzte ärztlich versorgt werden kann. Da sich beim zeichnerischen die 2 Geraden nicht schneiden komme ich da nicht weiter. Beim rechnerischen verstehe ich nichts.
2 Antworten
Entfernung des Krankenwagens vom Krankenhaus:
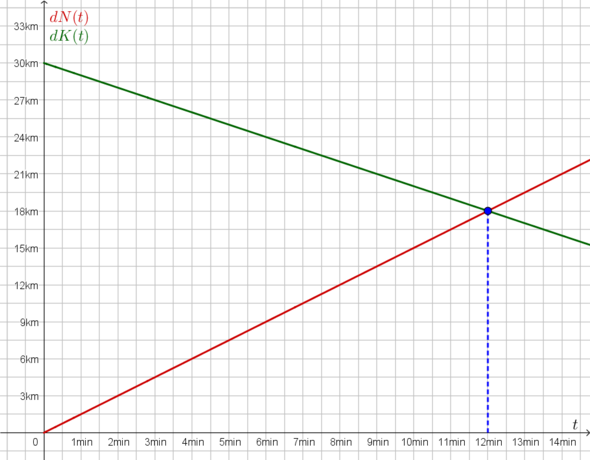
dK(t) = 30 km - 60 km/h * t
Entfernung des Notarztes vom Krankenhaus:
dN(t) = 90 km/h * t
Wann treffen sich Notarzt und Krankenwagen?
Wann ist also dN(t) = dK(t)?
Rechnerisch:
90 km/h * t = 30 km - 60 km/h * t
[Addition von 60 km/h * t]
150 km/h * t = 30 km
[Division durch 150 km/h]
t = 1/5 h = 1/5 * 60 min = 12 min
Notarzt und Krankenwagen treffen sich also 12 Minuten nach dem Losfahren.
Zeichnerisch: Bild im Anhang
[Für die Zeichnung ist es evtl. hilfreich sich zu überlegen, dass 60 km/h = 1 km/min bzw. 90 km/h = 1,5 km/min ist.]
Rechnerisch:
K(rankenwagen)
N(otarzt)
S(t, K) = 0km + 60 km/h * t
S(t, N) = 30km - 90 km/h * t
Die treffen sich dann logischerweise da, wo die beiden Gleichungen gleich sind. Also musst du sie gleichsetzen.
S(t, K) = S(t. N)
Da bekommst du die Zeit raus, zu der sie sich treffen. Diese Zeit dann in eine der Gleichungen eingesetzt, bekommst du den Ort raus, wo sie sich treffen.
Zur Kontrolle: Zeit t= 1/5 Stunden bzw. 12 min
Weg S(t) = 12 km
Woher weiss man dann die Steigung wenn man das zeichnen muss?