Warum Sinussatz nicht möglich?
Hallo Leute,
ich helfe jemandem bei seinen Mathe-Aufgaben und bei der b) funktioniert der Sinussatz nicht. Es sind doch aber ein Winkel und zwei Seiten gegeben, warum komme ich auf einen spitzen Winkel, obwohl dieser logischerweise stumpf sein müsste?

Vielen Dank für eure Antworten!
2 Antworten
Problem

das ist hier nicht gegeben , wenn du nicht auch DS berücksichtigst
nutzt man nur deine Angaben , erhält man alternativ zwei mögliche Dreiecke

und mit dem TR erwischt nur den kleineren der beiden möglichen Winkel
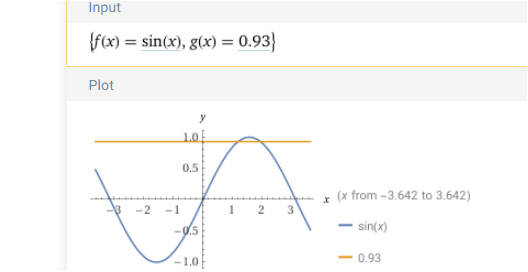
zu 0.93 gehören aber zwei Winkel

ist mir auch neu : aber nur mit cos kommt man hier auf die richtige Größe

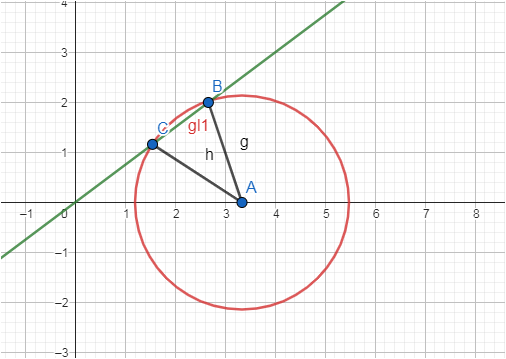
und woher weiß man definitiv bei dieser Aufgabe, dass die stumpfwinklige Variante gesucht ist ?
Aufgrund der Maße hat Hicksder1 in seiner Frage bereits angegeben, daß es sich um einen stumpfen Winkel handeln muß und dies zurecht: Es handelt sich um ein fast gleichschenkliges Dreieck mit einem Grundlinienwinkel von 37°. D.h. der andere Grundlinienwinkel Ist sogar kleiner als 37°.180°-2×37°=106°. Und dies ist ein stumpfer Winkel.
Und außerdem hat die Sinusfunktion y=sin(x) für ein bestimmtes y unendlich viele Lösungen, wobei für geometrische Probleme aber meist eine Lösung ausreicht. Aber es gibt auch Ausnahmen.
Übrigens: Deine graphischen Darstellungen sind phantastisch gut! 🌝
Im Dreieck BDS sind dir die Längen aller 3 Seiten bekannt und deshalb solltest du den Kosinussatz anwenden.
334^2 = 214^2 + 193^2 - 2*214*193*cos(Beta)
Das nach cos(Beta) umgestellt und ausgerechnet und es kommt für den cos(Beta) ein Wert von -0,3451527771 raus. Nun diesen Wert mit der cos^-1 Taste auf dem TR umrechnen in Beta= 110,2°.
Mit dem Sinussatz kann man die Lösung schon finden. Man muß nur bei stumpfwinkligen Dreicken folgendes beachten:
sin(x)=sin(180°-x)