Warum sind Wechselwinkel an parallelen Geraden gleich groß?
3 Antworten
Hallo,
siehe beigefügte Skizze:
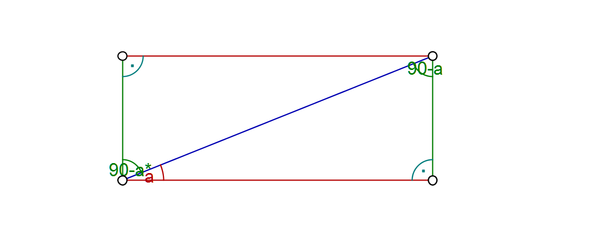
Die beiden Parallelen (rot), die von einem Strahl (blau) geschnitten werden, sind durch zwei Senkrechten (grün) zu einem Rechteck ergänzt worden.
Dieses Rechteck wird durch die blaue Diagonale (den Strahl) in zwei kongruente rechtwinklige Dreiecke geteilt.
Der Winkel 90°-a wird einmal durch a zu einem rechten Winkel ergänzt, andererseits ergänzt er die Innenwinkel des Dreiecks zusammen mit dem rechten Winkel und a zu 180°.
Herzliche Grüße,
Willy
Es ist schwierig da eine befriedigende Antwort zu geben.
Aus Symmetriegründen!
Stell dir eine unendliche lange Gerade vor. Jetzt nimmst du eine weitere unendlich lange Gerade und platzierst sie unter einem gewissen Winkel zu der Ersten. Fügst du nun eine dritte unend. l. Gerade hinzu, die parallel zur Zweiten ist, dann kannst du sie als Kopie jener interpretieren - Beide haben die gleiche Ausrichtung in einem unendlichen Raum.
Legst du diese beiden parallelen Geraden nebeneinander, dann kannst du immer eine der beiden abdecken (du hast dann 2 Bilder) und argumentieren, dass es sich in beiden Fällen um ein und die Selbe handelt. Warum? In einem unendlichen Raum mit zwei unendlichen langen Geraden kannst du die Position nicht wirklich definieren, es gibt ja keinen Anhaltspunkt. Betrachtest du die beiden Bilder oben, kannst du auch da keine Unterscheidung treffen, was schlussfolgert, dass beide gleich zur ersten Geraden ausgerichtet sind (das ist die Symmetrie, du kannst sie nicht unterscheiden und deshalb müssen sie die gleichen Eigenschaften haben).
Im letzten Absatz: Du legst sie parallel auf die erste Gerade - das ergibt deine Fragestellung.
Es gibt mehrere äquivalente Fassungen des Parallelenaxioms, welches selber bekanntlich nicht aus den übrigen Grundannahmen der Geometrie folgt.
ja, aber beim gängigen Beweis des Satzes über die Winkelsumme im Dreieck wird die Gleichheit der Wechselwinkel an parallelen Geraden benutzt.