Vollständige Induktion einer folge?
Ich wollte jetzt von der Folge die Beschränktheit beweisen mithilfe der vollständigen Induktion jedoch irritiert mich dieses a_n. Könnte mir vielleicht jemand helfen und mir sagen wie man das richtig schreibt ?
.
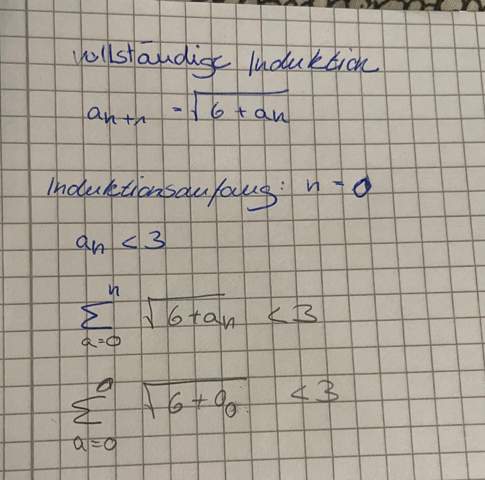
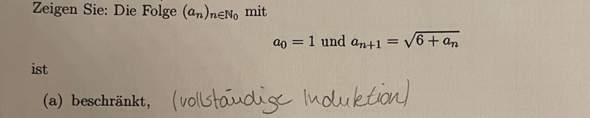
Wie kommst du auf die Idee mit der Summe?Das wäre dann ja eine Reihe.Oder? Außerdem ist doch dann die Frage, was a_0 ist.denn a_0 ist ja über a_{-1} definiert.Hast mal die Aufgabe?
Wir hatten bei folgen noch keine Induktion gemacht deshalb dachte ich das ich es so machen kann wie wir es vorher immer gemacht haben
3 Antworten
ok... geht doch.... also:
zu beweisen ist, dass die Folge beschränkt ist... versuchen wir mal, zu zeigen, dass sie durch 0 nach unten beschränkt ist, und durch 3 nach oben beschränkt ist...
die untere Schranke stimmt offensichtlich... wegen der Def. der Wurzelfunk... auch ohne Beweis sofort klar...
zu der oberen Schranke: wir versuchen es mit vollst. Ind.:
IA: a_0=1 < 3 fertig!
IV: a_n < 3 sei bereits bewiesen...
IS: gilt dann auch a_{n+1} < 3?
wegen der Monotonie der Wurzelfunktion...
q.e.d.
siehst du's jetzt?
Wenn ich jetzt den Grenzwert berechne also indem ich a=Wurzel 6+a nach a Auflösen komme ich einmal auf die obere Schranke also auf 3 und aber auch auf -2 wie kann ich jetzt begründen das -2 nicht geht?
Achtung, es gibt einen Unterschied zwischen Folgen und Reihen !
Eine Reihe ist die Aufsummierung der Folgenglieder.
Was genau willst zeigen?
Du musst nur zeigen, dass für alle n die Beträge aller Folgenglieder a_n kleiner als eine "Schranke" bleiben.
Ja so ergibt es auch Sinn. Was bedeutet q.e.d.? Vielen Dank 🙏