Vollständige induktion bei mengen?
Hallo Leute, ich muss auf meinen neuen AB eine Aufgabe zur Vollständigen Induktion lösen. Ich kann die vollständige induktion bei Summen usw aber bei dieser Aufgabe verzweifel ich und komme ehrlich kein Meter weiter. Kann mir jemand helfen und bitte so das es ein Ersti versteht :D
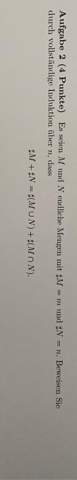
2 Antworten
A(m,n) = Aussage In Abhängigkeit von m, n
-----------------------------
A(m, n): #M + #N = #(MuN) + #(MnN)
m=0 und n=0:
A (0, 0): 0+0 = 0+0 .................wahre Aussage
____________________________________
zeige:
(1) A(m, n) → A(m+1, n) bzw. A(m, n) → A(m, n+1)
und
(2) A(m, n) → A(m+1, n+1)
---------------------------------------------
hier: A(m, n) → A(m+1, n+1)
neues Element von M = neues Element von N:
#M + #N = #(MuN) + #(MnN) → #M +1 #N +1 = #(MuN) +1 + #(MnN)+1
Äquivalenzumformung -2 auf der rechten Seite von →:
#M + #N = #(MuN) + #(MnN) → #M + #N = #(MuN) + #(MnN) ....wahre Aussage
-------------------------------------------------------------------------------------
neues Element von M ≠ neues Element von N
#M + #N = #(MuN) + #(MnN) → #M +1 #N +1 =#(MuN) +2 + #(MnN) + 0
Äquivalenzumformung -2 auf der rechten Seite von →:
#M + #N = #(MuN) + #(MnN) → #M + #N =#(MuN) + #(MnN)....wahre Aussage
_________
usw.
Also fange zunächst mit n=0 an, also N ist dann die Leere Menge, dort sollte es ziemlich klar sein, dass die Gleichheit gilt.
Induktionsvoraussetzung: die Aussage ist für ein beliebiges n wahr.
Induktionsschritt:
Betrachte nun den Fall n+1.
Das bedeutet, dass N jetzt ein Element mehr hat.
Somit kannst N so ausdrücken: N = N_alt vereinigt {x}, wobei x nicht in N_alt ist.
Betrachte nun die Fälle, ob x in M liegt oder nicht und nutze die Induktionsvoraussetzung um zu zeigen, dass die Rechte Seite nun den Wert n+1+m hat.