Vierfacher Münzwurf Wahrscheinlichkeitsrechnung?
Hallo Leute , ich habe Probleme damit diese Aufgaben zu verstehen.
Die Aufgabenstellung ist wie folgt:
Eine Münze wird viermal geworden. Schreiben Sie die Ergebnismengen auf.
Berechnen Sie die Wahrscheinlichkeit,dass
a) genau dreimal Kopf geworfen wird.
b) höchstens zweimal Zahl geworden wird.
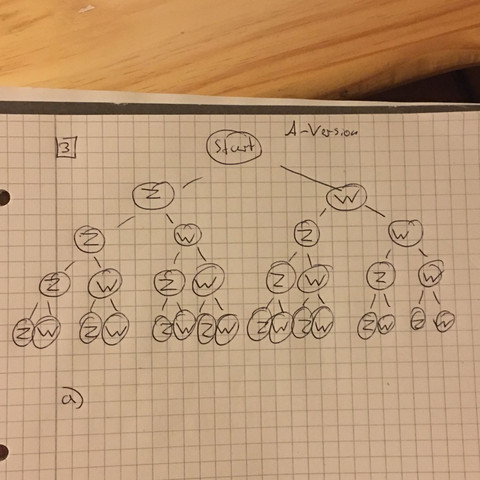
Ein Baumdiagramm habe ich zwar angefertigt bin mir aber nicht sicher ob das so stimmt.
Ich habe zwar schon unzählige Videos angesehen wurde daraus aber leider nicht wirklich schlauer.
3 Antworten

Der Baum ist korrekt (auch wenn ich nicht verstehe, warum du "Kopf" mit W bezeichnest).
Im nächsten Schritt solltest du aus dem Baum alle 16 Kombinationen (2^4) abschreiben - also von ZZZZ bis KKKK (oder WWWW, wenn dir das lieber ist).
Ich vermute mal, dass ihr die Formeln noch nicht durchgenommen habt und noch abzählt?
Dann zählst du ab, wie viele Kombinationen mit genau 3x K es gibt. Also ZKKK, KZKK, .... und teilst die Anzahl durch die Anzahl der möglichen Kombinationen.
Beim 2. Teil kannst du entweder abzählen, wie viele Kombinationen es mit höchstens 2x Z gibt (also 0x Z + 1x Z + 2x Z zusammen zählen) oder ...
(Und das ist der schlauere Ansatz)
Du negierst das Ereignis "höchstens 2x Z" - das Gegenteil ist dann "nicht 3x oder 4x Z" und ziehst diesen Wert von 1 (der Summe aller möglichen Ereignisse) ab.
4x Z kommt nur einmal vor, hat also die Wahrscheinlichkeit 1/16
3x Z kommt genau so häufig vor wie 3x K, also kannst du das Ergebnis aus Aufgabe a wieder verwenden.
Somit ist
P (höchstens 2x Z) = 1 - (1/16 + Ergebnis Aufgabe a)
Das solltest du ausrechnen können.


a. kannst du mit der "Bernoulli Formel" berechnen
P(X=K)=B(n;p;k)=(n/k)*p^k*(1-p)^(n-k)
hier ist k=3 und n=4 (Versuche)
p=1/2=0,5 also 0,5 Wahrscheinlichkeit,daß die Zahl kommt
(n/k)=n!/(k!*(n-k)!=4!/(3!*1!)=4 mögliche Pfade
P(3mal Zahl)=4*o,5^3*(1-0,5)^(4-3)=0,25 =25%
b. weiß ich nicht
HINWEIS: Beim "Bernoulliversuch" gibt es nur "Treffer" oder "Niete" (kommt oder kommt nich),bei "n" Versuchen und "k" Anzahl der Treffer.
Beispiel: Wie hoch ist die Wahrscheinlichkeit,daß beim Würfel n=4 (4 mal geworfen) genau 2 mal die 6 kommt?
k=2 und n=4 und p=1/6 eingesetzt
P(2*6)=4!/(2!*(4-2)!*(1/6)^2*(1-1/6)^(4-2)=0,1157=11,57%

a) 0,5^3
B)1-0,5^3

Danke für die Antwort
hätte dann bei a) 2*2*2*2=2⁴ = 16 4/16 = 0.25 (25%)
und bei b) P = 1- 5/16 = 11/16 = 0.68 raus
bin mir nicht wirklich sicher ob das richtig ist.