Unterschied numerische Integration zu normaler Integration?
servus. hab jetzt alle aufgaben fertig u. bin nun bei der letzten teilaufgabe angelangt, danke bis dahin für die tolle hilfe. Die letzte teilaufgabe lautet:
- diskutieren sie die differenz der berechneten werte vom numerischen integrieren (trapezregel: 4966,5 N; simpsonregel: 4962 N) u. dem rechnerischen integrieren ( 4962 N) was ist damit gemeint? schreiben das trapezregel ungenau ist? Einheit ist Newton ;)
3 Antworten
Ich habe es mal mit einer Programmiersprache ausprobiert, die mit 16 Stellen nach dem Komma rechnet.
Ich habe f(x) = sin(x) von 0 bis 6 integriert, mit der Trapezregel erhält man mit 100000 Unterteilungen -->
I = 0.03982971335 (gerundet)
Mit der Simpson-Regel nach 190 Unterteilungen -->
I = 0.03982971336 (gerundet)
Echter Wert --> 0.0398297133496340...
Die Trapezregel ist also etwas genauer, wenn man die maximalen Grenzen der jeweiligen Rechnergenauigkeit ausschöpft, als die Simpson-Regel, dafür werden aber auch sehr viel mehr Unterteilungen benötigt (526 mal mehr ist es hier).
Bei reinen, endlichen Polynomen bis zum Grad 3 ist die Simpsonregel genauer.
Das steht auch auf dieser Webseite -->
Das ist das Problem !!
Normalerweise ist die Trapezregel eben gerade NICHT (!!!) ungenau, im Vergleich zur Simpsonregel, sondern genauer als die Simpsonregel, aber deutlich aufwändiger.
Die Simpsonregel war nur in diesem speziellen Fall genauer, weil es sich um ein reines, endliches Polynom handelte, welches nicht größer als Grad 3 war !
wow, also kann ich zb. mal schreiben das simpson regel nur anwendbar bis polynom 3. grades ist? gilt das für die trapez regel auch?
Nein !! Die Simpsonregel ist immer anwendbar, außer wenn Definitionslücken vorhanden sind !
Vorteile -->
Schnelligkeit --> Simpsonregel
Genauigkeit --> Trapezregel, außer bei Polynomen bis zum Grad 3, da hat die Simpsonregel die Nase vorn
Gib mal bitte eine Quelle an, in der man lesen kann, dass die Trapezregel genauer als die Simpsonregel ist. Ich muss dich hierbei leider korrigieren, denn der Genauigkeitsgrad der Simpsonregel ist 3 und der der Trapezregel nur 1. Zudem solltest du dich von dem Gedanken loslösen, alles in der Mathematik mit dem Computer berechnen zu wollen, darum geht es nämlich nur in der numerischen Mathematik, die nur eines von mehreren Teilgebieten der Mathematik ist.
Die Trapezregel liefert nur bei Polynomen vom Höchstgrad 1 den exakten Wert des Integrals.
Ich habe jetzt noch mal f(x) = sin(x) von 0 bis 6 integriert, 16 Stellen Rechnergenauigkeit, mit der Trapezregel erhält man mit 100000 Unterteilungen -->
I = 0.03982971335 (gerundet)
Mit der Simpson-Regel nach 190 Unterteilungen -->
I = 0.03982971336 (gerundet)
Echter Wert --> 0.0398297133496340...
Die Trapezregel ist also etwas genauer, wenn man die maximalen Grenzen der jeweiligen Rechnergenauigkeit ausschöpft, als die Simpson-Regel, dafür werden aber auch sehr viel mehr Unterteilungen benötigt (526 mal mehr ist es hier).
Bei Polynomen bis zum Grad 3 ist die Simpsonregel genauer.
Das steht auch auf dieser Webseite -->
--------------------------------------------------------------------------------------
Außerdem habe ich nie behauptet alles mit dem Computer berechnen zu wollen :-)), aber die Trapezregel und die Simpsonregel gehören nun mal ins Teilgebiet der numerischen Mathematik, versuche mal 100000 Intervallunterteilungen per Hand zu berechnen :-)), das kannst du in dem Buch "Numerische Mathematik" von H.R. Schwarz aus dem Teubner-Verlag selber nachlesen, das steht auch drin, dass es noch wesentlich bessere Verfahren zur numerischen Integration gibt als nur die Trapezregel und das Simpson-Verfahren, dazu braucht man den Computer wenn man richtig genaue Ergebnisse haben will.
Ich dachte auch die trapezregel ist ungenauer, da man ja mit trapezen sich der kurve der funktion annähert u. dabei entsteht ja immer ein kleiner spalt in form eines dreiecks oder nicht? das ist doch mein "error" bzw. meine ungenauigkeit oder?
@ everysingleday1
Falls du es übersehen hast, ich habe geschrieben, dass ich die Funktion f(x) = sin(x) von 0 bis 6 integriert habe !! Die Ergebnisse beziehen sich darauf !
Ich kenne das Buch von Schwarz, da ich mich seit Monaten mit dem Thema auseinandersetze. Ein Blick in das Buch von Plato wäre ratsam, dort stehen viele Beweise zu den grundlegenden Erkenntnissen. Und es steht nunmal fest, dass die Simpson-Regel einen höheren Genauigkeitsgrad als die Trapezregel hat. Fest steht aber auch, dass die Trapezregel bei periodischen Funktionen so wie in diesem Fall effizienter ist. Das hat aber nichts mit deren geringem Genauigkeitsgrad zu tun.
.................
Das mit dem "alles mit dem Computer ausrechnen zu wollen" bezog sich eher auf deine Versuche, den Real- und den Imaginärteil von komplexen Zahlen den Computer rechnen lassen zu wollen. So etwas rechnet man immer per Hand, da es zu den Grundlagen in einem Mathematik-Studium zählt.
@ maximilian1990
Ich habe dir 2 Computerprogramme gegeben, eines zur Trapezregel und eines zu Simpson-Regel.
Probiere sie eigenständig und selber mithilfe von Funktionen aus, die KEINE (!!!) einfachen reinen Polynome bis zum Grad 3 sind, dann wirst du ja selber bemerken welches von den beiden Verfahren das genauere ist. Im Falle von sin(x) von 0 bis 6 integriert ist es die Trapezregel, kannst du selber nachprüfen !
Bei einer anderen Aufgabe, ich weiß nicht mehr welche, habe ich alles lieb und brav per Hand gemacht :-)), ich mache es also nicht immer mit dem Computer :-))
... aber doch sehr oft, wie mir scheint. Meiner Meinung nach ist damit auf gutefrage.net den meisten Fragestellern nicht geholfen. Erstens können die meisten von ihnen nicht programmieren, zweitens haben sie in ihren Klausuren keinen Rechner vor sich stehen, den sie nutzen könnten.
Das finde ich sehr schade ;-((
Es gibt nun mal Bereiche im Leben da kommt man um numerische Mathematik nicht herum, vorallem dann nicht, wenn man nicht riesig lange Zeit für Handberechnungen übrig hat.
entsteht die ungenauigkeit jetzt durch den spalt an der funktion?
Welche Funktion meinst du jetzt genau und welchen Spalt ?
So ein Mathematikstudium ist nunmal zeitaufwendig, das merkt man schon mit Beginn des Studiums im 1. Semester. Und auch die Ingenieure müssen ihre Klausuren an den Universitäten ohne Hilfsmittel bestehen. Da sind noch nicht mal Taschenrechner zugelassen.
bei der annäherung durch die trapeze an die kurve der funktion entsteht ja immer ein dreieck. diesen spalt mein ich
Ok, aber wenn sie ihr Studium fertig haben, dann setzen sie aber numerische Mathematik ein.
Wettervorhersagen
Nichtlineare Regression
Differentialgleichungssysteme, auch partielle
Eigenwertberechnung von sehr großen Matrizen
Berechnung von Sternmodellen in der Astrophysik
Strömumgsmodelle
Berechnung von riesigen linearen Gleichungssystemen mittels Iteration
Spline-Interpolation
usw.
Das ist ja alles ohne numerische Mathematik und Computer praktisch nicht berechenbar.
Du hattest ja gesehen, dass deine eine Funktion auch mit der Trapezregel schon aus 7 Stellen nach dem Komma genau war, das ist ja nicht ungenau. Die Simpson-Regel war nur einfach genauer, weil es ein Polynom 3-ten Grades war.
Die Simpson-Regel ist gut, weil sie schneller ist.
Exakt so ist es, sofern diese Mathematiker den Weg in das Spezialgebiet der numerischen Mathematik gehen. Falls nicht, werden sie weiterhin mit Stift und Papier hantieren.
Mit 100000 Unterteilungen war es auf 7 Stellen nach dem Komma genau !
"normale" Integration bedeutet symbolisch integrieren:
zu primitiven Funktionen sind Integrationsregeln bekannt (Mathebücher mit Listen von Tabellen) , d.h. man hat als Ergebnis eine fertige Funktion, die man beliebig genau berechnen kann. (Polynome, sin,...)
Oft sind aber die Integrationsfunktionen nicht bekannt und so bleiben nur numerische Algorithmen. Hier muss man die gewünschte Genauigkeit vorgeben und so lange rechnen, bis diese erreicht wird.
Unter http://www.gerdlamprecht.de/Integral_Substitutionen.html
§B1b ist das Integral t^t dt bis zur Grenze x, was bis heute nicht symbolisch integrierbar ist! Selbst die Wandlung in unendliche Summe benötigt die ExpIntegralE-Funktion, die auch wieder eine Integralfunktion ist, die nur aus unendlichen Summen (hypergeometrischen Funktionen) berechnet werden kann.
Das Problem bei numerischen Methoden ist der Rechenaufwand und der verwendete Variablentyp. 99% der Programme verwenden double, was nur 15 Stellen genau ist. Wenn man nun große Bereichsgrenzen hat, wird die Anzahl der kleinen Flächenstücke sehr groß. Beim Aufsummieren summiert sich auch der Rundungsfehler (Fehlerfortpflanzung).
Vergleich numerischer Methoden wird oft falsch herangegangen. Man nimmt eine konstante Anzahl an Flächenstücken (hast Du leider nicht angegeben) und vergleicht das Ergebnis.
Unter Wissenschaftlern gibt man die gesuchte Genauigkeit vor (denn 99% aller echten Ergebnisse sind irrational und haben unendlich viele Stellen).
Nun sucht man den geeignetsten Algorithmus, der am schnellsten zum Ergebnis kommt, denn das kann zwischen Sekunden und Tagen schwanken.
Trapezregel ist bei gleicher Anzahl an Teilflächen zur Simpsonregel deshalb ungenauer, weil hier nur geradlinige Verbindungslinien verwendet werden.
Bei Simpsonregel wird ein Interpolationspolynom als Teilfläche verwendet. Logisch, dass das dann genauer ist, wenn Ihr Polynome als Integrationsfunktion verwendet!
Wikipedia: Simpsonregel
Wie man bei DepravedGirl sieht, kommen mehrere Fakten zusammen:
- Rundungsfehler kann auch mal positive Auswirkung haben
- 100000 Teilstücke werden mit 190 verglichen
hab mal ein bild angefügt u. zwschen x2 u. x3 die stelle markiert die ich mein also den "spalt". ich denke dadurch entsteht eben eine ungenauigkeit oder
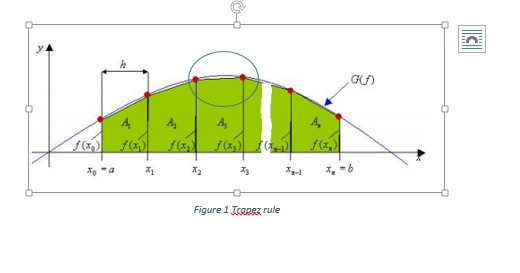
Ja, und wenn Du uns noch die genaue Funktion mit den Randgrenzen verraten würdest, könnte man diesen "Spalt" (besser Flächenstück) beliebig genau ausrechnen.
Wie gesagt: für Polynome braucht man keine umständliche Numerik, da die Integralfunktionen bekannt sind.
Für komplizierte Funktionen gibt es oft bessere Verfahren wie
Tanh-sinh_quadrature (siehe engl. Wikipedia)
http://www.gerdlamprecht.de/Roemisch_JAVA.htm
zeigt im Beispiel 80, wie man
sqrt((1-x*x)*(1-x*x/2)) von 0...1 {sqrt = Wurzel}
bei nur 1024 Iterationen auf alle 16 Nachkommastellen genau berechnen kann!
(exakter Wert: EllipticE(1/2)-(EllipticK(1/2))/3
= 0.732618988613884863042224619606972492610322759... )
Hinweis: Viele Taschenrechner können oft nicht mal sin(22) auf 8 Stellen genau berechnen, da wegen des Preises auch nur Näherungen statt echte Reihenentwicklung verwendet werden.
ok danke, aber kann schlecht schreiben das mit der programmiersprache sowas rausgefunden habe ;) meine ergebnisse stimme ja oder ? also normale integration 4962, trapez 4966,5 u. simpson 4962? somit wäre ja trapez sehr ungenau?