Lineare Funktion?
Übung (P1(4/6); P2(-2/4)
müssen daraus F(x)=mx+b Berechnen..
kann mir jemand helfen ???
3 Antworten
Als erstes prüfst du welcher Punkt links und welcher rechts liegt. Punkt P2 liegt links weil die x-Koordinate x = -2 ist und die Zahl kleiner ist als die x- Koordinate von Punkt P1 die ja x = 4 ist
Der linke Punkt bekommt hat immer x1 als Bezeichnung und der rechte Punkt hat x2 als Bezeichnung.
x1 = -2 (von P2) und x2 = 4 (von P1)
Jetzt die y-Koordinate raussuchen
y1 = 4 (von P2) und y2 = 6 (von P1)
Nun die Steigung mit der Formel bestimmt
Jetzt einsetzen in f(x) = mx + b
f(x) = 1/3 * x + b
Nun einen Punkt aussuchen und einsetzen. Ich habe mir P1(4|6) ausgesucht und setze ein mit x = 4 und f(x) = 6
6 = 1/3 * 4 + b
Jetzt nach b auflösen
6 = 4/3 + b
6 - 4/3 = b
b = 4,66
Funktion f(x) = 1/3 * x + 4,66

Theoretisch darfst du auflösen, aber es ist genauer, wenn du 1/3 schreibst, denn 1/3 ist ja eigentlich 0,333333333... und nicht nur 0,33
Kannst du mir auch die Zeichnung erklären ?
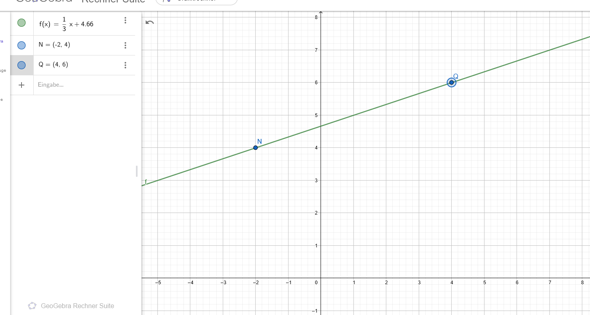
Na die Zeichnung zeigt deine Funktion. F(x)=mx+b beschreibt eine Gerade. Also eine Linie durch deine 2 Punkte. Die zwei Punkte siehst du auch in der Zeichnung, wobei die hier N und Q heißen.
Tipp:
m ist immer deine Steigung. Dort siehst du also, ob die Gerade von links nach rechts steigt oder sinkt, bzw. wie stark sie steigt oder sinkt.
Den Wert für die Steigung m erhältst Du am einfachsten durch die Differenz der y-Koordinaten geteilt durch die Differenz der x-Koordinaten.
Du hast also
P1(4/6)
P2(-2/4)
Also
Δy/Δx=(4-6)/(-2-4)=-2/-6=⅓
Hier musst du auch gar nicht prüfen, welcher Punkt wo links oder rechts liegt, das Verfahren geht auch umgekehrt:
Δy/Δx=(6-4)/(4-(-2))=2/(4+2)=2/6=⅓
Damit kannst Du schon mal schreiben
f(x)=⅓x+b
Du setzt einen der Punkte in die Gleichung ein:
6=⅓*4+b
b=6-1⅓=4⅔
somit
f(x)=⅓x+4⅔
Gegenprobe mit zweitem Punkt
4=⅓*(-2)+4⅔
4=-⅔+4⅔
4=4
Uiii, es stimmt!
Man kann beide Punkte in die allgemeine Form einsetzen und erhält ein LGS mit zwei Gleichungen und zwei Unbekannten (m und b). Nun löst man das LGS, erhält m und b und setzt diese in die allgemeine Form ein.
Habe als Ergebnis 4,33 gehabt als ich alleine gerechnet habe