Sind die Punkte A und B die Nullstellen?
Hallo :) bin gerade bei einer neuen Mathe Aufgabe und wie man an meinen vorherigen fragen sieht habe ich da meine Probleme..
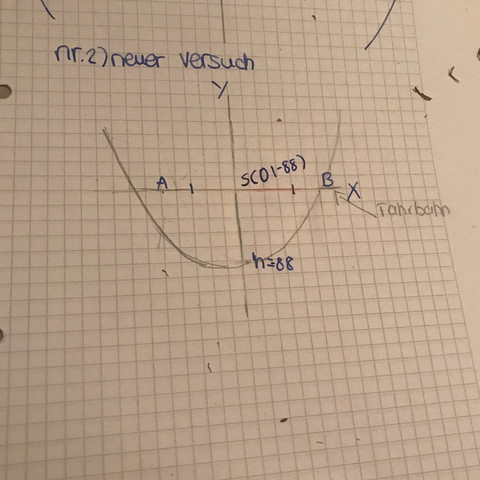
Nun steht ja in der Aufgabe das man A und B herausfinden soll.. sind das sozusagen die nullstellen?? Und
Und ist mein Koordinatensystem schon richtig??
Ist nur ne Skizze

4 Antworten
Die Nullstellen wären die Punkte A und B ja nur, wenn hier f(xa) = 0 und f(xb) = 0 wären, aber man kann graphisch ja gut erkennen, dass die Funktion oberhalb der Abszisse (meist x-Achse genannt) liegt. Ist dies der Fall "durchstößen" die "Arme" der Parabel auch nicht die Abszisse, also kann es keine Nullstellen geben. Betrachtet man die Funktionsgleichung f(x) = ax^2 ist das auch klar :)
Die Höhe der Punkte, also die y-Koordinate ist mit 88m gegeben.
Der Abstand der beiden Punkte ist ebenfalls gegeben und zwar durch die Spannweite von 486m
Wenn die Funktion also durch den Koordinatenursprung (0|0) geht, dann befindet sich A bei der x-Koordinate x= -243 und der Punkt B bei der x-Koordinate x = 243
Damit hätten wir schon die Punkte bestimmt:
=> A(-243|88) und B(243|88)
Für die Entwerfung einer Funktionsgleichung den Ansatz f(x) = ax^2 nutzen
Mit den Bedingungen a = positiv ; f(-243) = 88 ; f(243) = 88
Viel Erfolg weiterhin ;)
Und ist mein Koordinatensystem schon richtig??
Nein, dein KS gehört zu einer Parabel der Form
f(x) = ax² + b
wobei das b hier negativ wäre
und die Punkte A und B liegen auf der x-Achse, hätten eine Höhe von 0 ( Null ) also . So kann es nicht stimmen. Was stimmt ist nur der Maßstab der Parabel, die nach unten verschoben ist.
Der Scheitelpunkt liegt bei dir bei ( 0 / - 88 ) , der Punkt A bei ( - 243 / 0 ) , der Punkt B bei ( 243 / 0 ) .
Um nun auf die Glg zu kommen müsstest du y = ax² + b nutzen und hättest zwei Glg. zu lösen.
-88 = a * 0² + b >>>>>>>>>>>> - 88 = b
und
0 = a * -243² + b ( = -88 )
88/243² = a = 0,00149028773
Deine Parabel hieße y = 0,00149028773 * x² - 88
Macht das Sinn ? Nein, denn setzt du 243 ein , erhälst du Null und das ist nicht die Höhe von Punkt B.
Man kann A und B ohne Probleme ablesen, die x - Achse läuft durch den Scheitelpunkt
und für die Funktionsgleichung setzt man entweder A ( - 243 / 88 ) oder B ( 243 / 88 ) ein
88 = a * 243² oder 88 = a * -243²
macht beide male
a =0,00149028773
Deine Glg hieße also
y = 0,00149028773 * x²
mit x = 243 oder -243 wird ihre Höhe dort 88
Nein, nicht in dem hier verwendeten Koordinatensystem.
Die Funktion ist ja angegeben: f(x) = a*x²
Die (doppelte) Nullstelle ist hier der Scheitelpunkt.
Kannst du so machen.
Ja, der Kommentar bezog sich nur darauf, dass die Skizze in Ordnung war. Auf mehr nicht.
Also sind A und B einfach nur irgendwelche Koordinaten und das heißt diese Parabel hat nur eine Nullstelle oder??