Physik Induktionsgesetz Aufgabe?
Ich bräuchte dringend Hilfe bei folgender Aufgabe
Eine kreisförmige Leiterschleife (d=6,5cm) liegt in einem homogenen Magnetfeld der Stärke B= 33mT . Berechnen Sie den magnetischen Fluss für die Fälle, dass der Winkel zwischen der Leiterschleife und der Feldstärke ~B a.) 90°, b.) 60° ,c.) 45°, d.)0° und e.) 180° beträgt.
Mein Ansatz für die Aufgabe wäre ja zuerst den Durchmesser in Radius umwandeln und dann in Meter umzurechen und anschließend noch die 33mT in T umwandeln. Dann würde ich die Kreisfläche mit A=Pi * r² berechen.
Jedoch bin ich mir nicht sicher ob ich dann den magnetischen Fluss mit
Φ= BAcos(winkel)
oder mit
Φ=BAsin(winkel)
berechnen soll.
Kann mir jemand sagen ob die Schritte die ich bis ich jetzt gemacht alle richtig sind und ob ich mit sinus oder cosinus rechnen soll.
Danke im vorraus
3 Antworten
Es gilt hier in diesem Falle:
Phi = A(w)*B mit Winkel w
A(w) ist hierbei die orthogonal zum B-Feld stehende eingeschlossene Fläche der Ringschleife. Liegt die Ringschleife "flach" (w = 0°) so gilt für die Fläche
A(0°) = A(Kreis) = pi*(d/2)^2
Zeichnet man sich nun die Lage der Fläche schematisch für "beliebige" Winkel w auf, so folgt der senkrecht Anteil A(w) zu
A(w) = A(0°)*cos(w)
Damit folgt der magnetische Fluss durch die Schleife zu
Phi = cos(w)*B*pi*(d/2)^2
Hallo MaximMaximal,
was in der Aufgabenstellung als „Feldstärke“ bezeichnet wird, also B› (es ist eine Vektorgröße, eine Größe mit Richtung), heißt üblicherweise magnetische Flussdichte.
Damit kommt auch besser zum Ausdruck, dass der Fluss das Produkt aus B› und der vom Feld „durchströmten“ Fläche A ist.
Man kann die Fläche selbst als Vektor
(1) A› = A·n›
beschreiben, wobei mit n› hier ein Normaleneinheitsvektor gemeint ist, d.h., er gibt lediglich eine Richtung an, nämlich (lokal) senkrecht zur Fläche. Dann ist der Fluss - falls B› und n› konstant sind -
(2.1) Φ = ‹A,B› = A‹n,B›,
wobei '‹a,b›' das Skalarprodukt der Vektoren a› und b› ist. Bilden die den Winkel φ, so ist
(2.2) Φ = |A›|·|B›|·cos(φ).
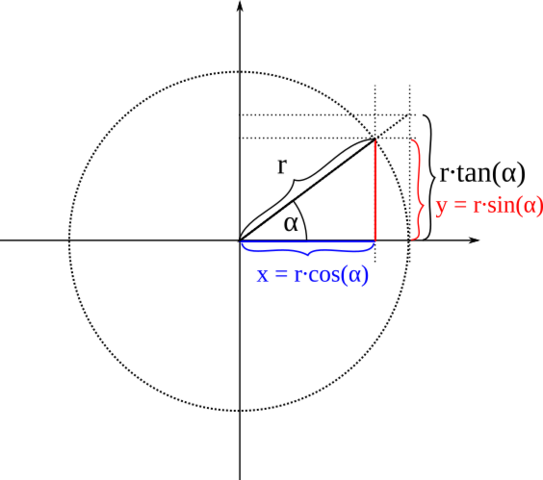
Dabei ist aber zu beachten, dass der Normalenvektor selbst senkrecht zur Schleifenfläche steht. Wenn es um den Winkel α zur Leiterschleife selbst geht, musst Du den Sinus nehmen.
Brauchen wir noch A. Du hast einen Durchmesser d und einen Radius r=d/h, und somit ist
(3) Α = πr² = πd²/4 ≈ (11/14)d².
Wenn Du vor der Rechnung alles in SI-Einheiten umrechnest, bekommst Du Φ in Wb (Weber).
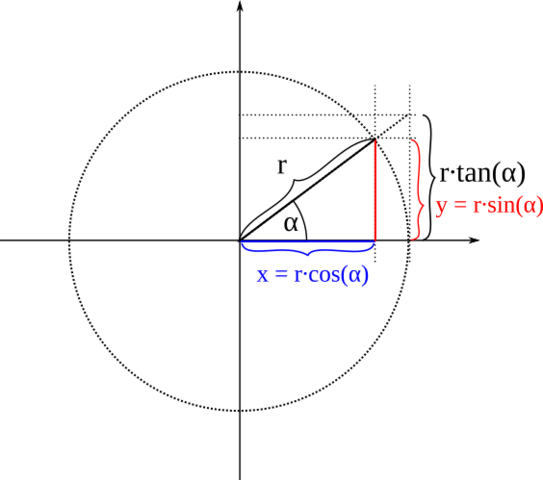
Deine Schritte sind richtig, vor allem vergessen viele in SI Einheiten umzuwandeln. Und auch der Ansatz mit sin, bzw.cos weiterzumachen stimmt natl!
Die Entscheidung bei ob Sin oder Cos fällt, eigentlich immer recht leicht! Denk an den Verlauf der beiden Funktionen und frag Dich bei welchem Winkel der Wert maximal, also 100 %, bzw der WinkelFaktor 1,00 sein muss?