Normalverteilung?

kann mir jemand helfen? Danke

ist hier die Antwort c richtig?

Answer 1

[mihisu]

Man kann sich dazu merken, dass bei einer normalverteilten Größe...

• etwa 68 % der Werte höchstens eine Standardabweichung vom Mittelwert abweichen.
• etwa 95 % der Werte höchstens zwei Standardabweichungen vom Mittelwert abweichen.
• etwa 99,7 % der Werte höchstens drei Standardabweichungen vom Mittelwert abweichen.
• Die Verteilung ist symmetrisch um den Mittelwert. 50 % der Werte sind kleiner als der Mittelwert. 50 % der Werte sind größer als der Mittelwert.

Im konkreten Fall erhält man damit grob...

$P(X<16\,\text{cm})\approx 50\,\%+\frac{68\,\%}{2}=84\,\%$

$P(12\,\text{cm}<X<16\,\text{cm})\approx 68\,\%$

$P(X>20\,\text{cm})\approx \frac{100\,\%-99\text{,}7\,\%}{2}=0\text{,}15\,\%$

$P(X<12\,\text{cm})\approx \frac{100\,\%-68\,\%}{2}=16\,\%$

$P(X>20\,\text{cm})\approx \frac{100\,\%-99\text{,}7\,\%}{2}=0\text{,}15\,\%$

Damit ist dann die dritte Antwortmöglichkeit richtig. Denn „größer als 20 cm“ bedeutet hier wegen 20 = 14 + 3 ⋅ 2, dass der Messwert um mehr als 3 Standardabweichungen nach oben vom Mittelwert abweicht. Es weichen etwa 100 % - 99,7 % = 0,3 % der Messwerte um mehr als 3 Standardabweichungen vom Messwert ab. Wenn man nur die nach oben abweichenden Messwerte möchte (und nicht auch die nach unten abweichenden), muss man diesen Prozentwert noch halbieren und erhält dann die angegebenen 0,15 %.

Answer 2

[indiachinacook]

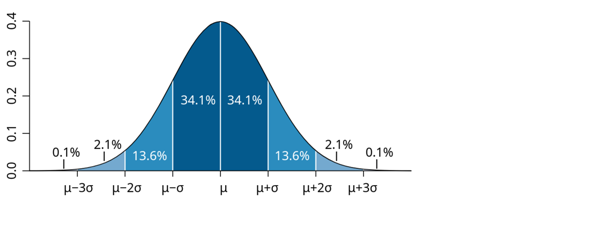
Man merkt sich am besten das folgende Diagramm:

In Deinem Fall ist der Mittelwert µ=14 und die Standardabweichung σ=2. Also:

1. In der ersten Frage soll man herausfinden, wie groß die Wahrscheinlichkeit für einen Meßwert kleiner als 16 ist, also μ+σ. Das ist die linke Hälfte der Kurve (50%) plus dem dunkelblauen Anteil rechts (34.1%), also ≈84%. Die Antwort ist also falsch.
2. in der zweiten Frage geht es um den Längenbereich 12–16 cm, also μ±σ. Das ist genau der dunkelblaue Anteil, also ≈68%. Die Antwort ist also auch falsch.
3. Größer als 20 cm heißt mehr als 3σ Abweichung nach oben (der kleine Schwanz in der Kurve rechts). Das sind ca. 0.1%, also stimmt die Antwort.
4. Kleiner als 12 cm heißt kleiner als μ−σ. Wenn Du auf der linken Seite der Kurve aufaddierst, dann bekommst Du 0.1+2.1+13.6=15.8%, das stimmt also wieder nicht.
5. Die letzte Aussage muß auch falsch sein, weil wir das bereits in der dritten Frage geklärt haben.

Deine Vermutung, daß (3) die einzig richtige Antwort ist, trifft also zu.

Answer 3

[Wechselfreund]

Ich denke schon. Innerhalb einer 3 sigma umgebung liegen 99,7%, die Hälfte des Wertes außerhalb ist also 0,15%.