Netwerkgleichungen?

Ich soll für dieses Netzwerk mittels Kirchhoffscher Regeln die Netzwerkgleichungen aufstellen! Weiß jemand wie das geht? Ich schaffe es nicht alle nötigen Gleichungen zu finden.

Answer 1

[mihisu]

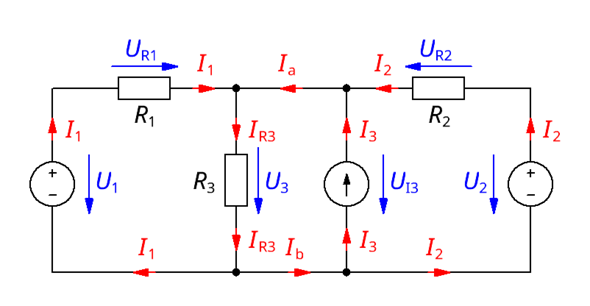
Zunächst einmal würde ich noch entsprechend weitere Bezeichnungen für Spannungen und Stromstärken ergänzen.

Dann kann man die entsprechenden Maschen und Knoten markieren...

... und dann systematisch die Maschen und Knoten abarbeiten; sowie die Beziehung zwischen Widerstand, Spannung und Stromstärke an den Widerständen angeben.

Damit erhält man dann die folgenden Gleichungen:

$\left[\text{M}_1\right]:\quad U_1-U_3-U_{\text{R}1}=0$

$\left[\text{M}_2\right]:\quad U_3-U_{\text{I}3}=0$

$\left[\text{M}_3\right]:\quad U_{\text{I}3}-U_2+U_{\text{R}2}=0$

$\left[\text{K}_1\right]:\quad I_{1}+I_{\text{a}}-I_{\text{R}3}=0$

$\left[\text{K}_2\right]:\quad I_{2}+I_{3}-I_{\text{a}}=0$

$\left[\text{K}_3\right]:\quad I_{\text{R}3}-I_{1}-I_{\text{b}}=0$

$\left[\text{K}_4\right]:\quad I_{\text{b}}-I_{3}-I_{2}=0$

$\left[\text{R}_1\right]:\quad U_{\text{R}1}=R_{1}\cdot I_{1}$

$\left[\text{R}_2\right]:\quad U_{\text{R}2}=R_{2}\cdot I_{2}$

$\left[\text{R}_3\right]:\quad U_{3}=R_{3}\cdot I_{\text{R}3}$

Damit hast du dann alle Gleichungen gegeben. [Wobei eine der Knotengleichungen eigentlich überflüssig ist, da sich diese auch rechnerisch aus den anderen Knotengleichungen ergibt.]

Hat das dir geholfen?
Wenn nicht: Kannst du genauer beschreiben, wo bei dir das Problem liegt? (Die Maschen erkennen? Die Knoten erkennen? Sonstige Probleme?)

Comments

[Rahov]

Danke für deine Antwort, kurze Frage noch: Sind nicht zwei der Knoten und eine der Maschen bei dir linear abhängig?

[mihisu]

@Rahov

Nein, bei den Maschen habe ich keine lineare Abhängigkeit, so wie ich diese aufgestellt habe. Wo siehst du da eine lineare Abhängigkeit?

Aber, ja... Bei den Knotengleichungen ist aber eine lineare Abhängigkeit gegeben. Eine der Knotengleichungen kann man als Linearkombination der anderen drei Gleichungen darstellen. Deshalb könnte man eine der Gleichungen weglassen. Es ist [K₁] + [K₂] + [K₃] + [K₄] = 0 und dementsprechend beispielsweise [K₄] = -([K₁] + [K₂] + [K₃]), sodass man beispielsweise [K₄] weglassen könnte. (Das hat man eigentlich immer bei solchen geschlossenen Netzwerken, dass man eine der Knotengleichungen weglassen kann, wenn man alle Knotengleichungen aufgestellt hat.) Das habe ich aber auch bereits in meiner Antwort geschrieben...

Damit hast du dann alle Gleichungen gegeben. [Wobei eine der Knotengleichungen eigentlich überflüssig ist, da sich diese auch rechnerisch aus den anderen Knotengleichungen ergibt.]

Bei den Maschen tritt dieser Effekt so nicht auf, da man üblicherweise gar nicht daran denkt, die eigentlich zusätzlich noch vorhandene Masche (welche sich außen um das Netzwerk herum befindet, quasi um Unendlich als Mittelpunkt herum) zu betrachten.