n-tes Taylorpolynom von ln(2x-2)?
Hallo,
Ich sitze jetzt schon eine Weile über diese Aufgabe: Bilde das n-te Taylorpolynom von ln(2x-2) und komme nicht weiter. Ich habe nur eine Reihe gefunden die aber nicht für n=0 und n=1 zutrifft.
Wäre dankbar für einen tipp/lösung/erklärung.
Schönes Wochenende euch
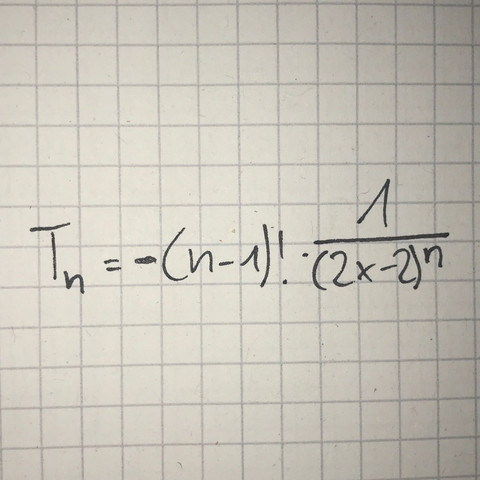
2 Antworten
Hallo,
letztlich geht es darum, eine Formel für die n. Ableitung zu finden - der Rest ist dann einfach.
Ableitung von ln (2x-2) ist nach der Kettenregel (innere mal äüßere Ableitung)
2*1/(2x-2), was durch 2 gekürzt werden kann zu 1/(x-1) oder (x-1)^(-1).
Da die innere Ableitung von x-1 immer 1 bleibt und sich an diesem Term bei weiteren Ableitungen auch nichts mehr ändert, kannst Du die weiteren Ableitungen ganz einfach nach der Potenzregel bilden:
f''=(-1)*(x-1)^(-2); f'''=(-2)*(-1)*(x-1)^(-3); f'''=(-3)*(-2)*(-1)*(x-1)^(-4).
Die Faktoren vor (x-1) sind also n! mit alternierenden Vorzeichen, während der Exponent n-1 entspricht.
Die alternierenden Vorzeichen kannst Du durch (-1)^n festlegen, das bei ungeraden n negativ, bei geraden n positiv wird.
Die n. Ableitung wäre demnach (-1)^n!*(x-1)^(-n-1).
Die vierte Ableitung lautete also 24*(x-1)^(-5) und die fünfte -120*(x-1)^(-6).
Jetzt sollte es einfach sein, das entsprechende Polynom auszurechnen.
Herzliche Grüße,
Willy
Stimmt, ich habe eben von (x-1)^(-1) an gerechnet, aber das ist ja bereits die erste Ableitung und nicht mehr die Funktion.
Dann lautet die Formel (-1)^(n-1)*(n-1)!*(x-1)^(-n)
ich weiß nur, dass es für den logarithmus naturalis eine taylorreihe für 0<x<=2 gibt, die lautete
(unend.)Σn=1 (-1)^(n+1)/n *(x-1)^n vielleicht einfach "2x-2" in das x einfügen und schreiben x element R mit 1<x<=2
vielen dank ich habe soweit alles verstanden. Eine Sache blieb unklar: die faktoren vor (x-1) sind doch (n-1)! und der exponent=n. Du hast es aber umgekehrt geschrieben. war das versehen oder verstehe ich etwas noch nicht?
vielen dank und grüße