Momentane Änderungsrate nach 5 Stunden?
Ich habe diesen Graph gegeben und muss die momentane Änderungsrate der Konzentration nach 5 Stunden angeben.
Ich habe da nach gefragt und das einfache Ablesen am Graph ist nicht erlaubt, ich muss eine Tangentensteigung zeichnen - also diese geradene Linie die den Graph berührt.
Ich möchte das aber nicht mit Steigungsdreieck usw. Wie kann ich das mit zwei Punkten lösen? Oder geht das nicht anders
hast du die Formel für den Graphen?
es ist nur diese Funktion gegeben, keine Formel
5 Antworten
Zwei Punkte: A und B
m = Δy / Δx = (0,4 - 2) / (6 - 3) = -1,6 / 3 = -0,53
Ergebnis: die momentane Änderungsrate beträgt -0,53 mg/(L*h)
Angenommen man wählt zwei Punkte auf dem Graphen vor und nach x = 5, dann kann man eine Gerade ziehen.
Nutzt aber nichts, weil nach der Steigung der Geraden gefragt ist. Angenomen die Punkte lauten P=(Px,Py) und Q=(Qx.Qy), dann ist die Steigung der Geraden gegeben durch
m = (Qy-Py)/(Qx-Px)
führt also doch wieder zu einem "Steigungsdreieck".
Ja, das stimmt näherungsweise, und beruht auf dem Prinzip eines Steigungsdreiecks m = (f(b) - f(a))/(b-a)
ich dachte die formel ist für die mittlere Änderungsrate hmm
Stimmt, das ändert aber nichts am Prinzip. Da der Graph nicht als Funktion gegeben ist, kann man zeichnerisch nur eine mittlere Änderungsrate bestimmen.
Geht das nicht mit nem Steigungsdreieck und dann einfach Y/X? ohne dieser FOrmel
Die Formal lautet nicht einfach y/x, sondern (y2 - y1)/(x2 - x1) mit den beiden Punkten (x1,y1) und (x2,y2). Ob man stattdessen (f(b) - f(a))/(b-a) oder (Qy-Py)/(Qx-Px) schreibt, spielt keine Rolle. Es ist immer dasselbe und läuft auf ein Steigungsdreieck hinaus.
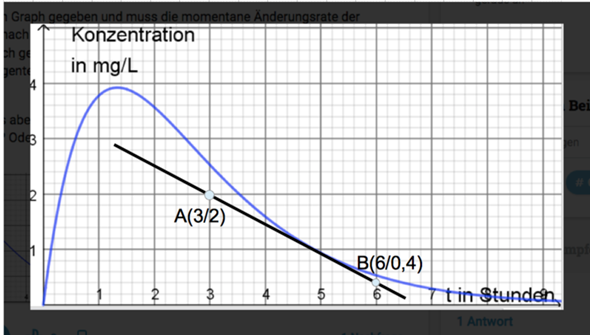
Die Koordinaten der zwei Punkte führen letztendlich auf den Term vom Steigungsdreieck.
Was heißt, "das einfache Ablesen am Graph ist nicht erlaubt"? Es ist schlicht nicht möglich. Denn die Änderungsrate der Konzentration ist die Steigung deines Graphen. Wenn du nur den Graph und keine Funktionsgleichung hast, musst du die Tangete (hier bei t=5) einzeichnen.
Wie du dann die Steigung dieser Tangente bestimmst, ist deine Sache. Steigungsdreieck ist das direkteste. Du darfst dir aber auch zwei beliebige Punkte auf der Tangente aussuchen, die ablesen und daraus die Steigung berechnen. Vom Prinzip her ist das eh das gleiche.
Naja ich dachte die mom. Änderungsrate ist einfach die Steigung an einer bestimmten Stelle
Wenn du die Funktion hast dann einfach ableiten und 5 einsetzten in die Ableitung dann hast du dein Ergebnis
Ich habe mal eines gezeichnet von 4 bis 6 rüber also ein Dreieck wo die Tangente bei x=5 den Graph berührt. Ok dann hab ich mal y/x gerechnet also 1,1 durch 2 = 0,55. kann das stimmen?