Mit welcher Methode bestimme ich Konvergenz, Divergenz und Grenzwerte am besten?
Moin Leute
Ich schreibe bald ne Klausur in Mathe und Muss Konvergenz Divergenz und Grenzwerte (von Reihen) zeigen bzw ausrechnen können. Nun haben wir dafür verschiedene Kriterien zur Verfügung. Meistens endet eine Aufgabe die ich zu lösen Versuche darin, das ich ein paar Kriterien ausprobiere und gucke ob diese zu einem Ergebnis führen. Da dies allerdings Zeitaufwendig ist, wollte ich fragen ob es eine Universalmethode für diese Aufgaben gibt?
Als Beispiel habe ich im Anhang eine Reihe eingefügt. Hier würde ich zuerst das Leibnitz Kriterium (wegen der -1) anwenden.
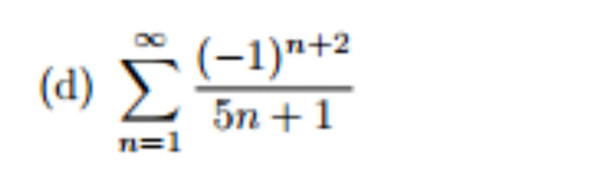
Wie würdet ihr das machen?
3 Antworten
Folgende zwei weitere Ideen:
- Zähler und Nenner gesondert untersuchen
- Untersuchen, ob die Folge kleiner / größer als eine andere Folge ist, deren Konvergenz man kennt. Wenn man z.B. die Folge 1/(n+1) hat und die Konvergenz von 1/n kennt, dann weiß man, dass 1/(n+1) < 1/n und somit die Folge 1/(n+1) zwischen der Folge 1/n und der 0 verläuft und damit selbst gegen 0 konvergiert.
Die gibt es wohl genauso wenig es keine allgemein gültige Integrationsmethode gibt.
Wenn man schon alle kennt, es gibt ja auch schwierige Konvergenz-Probleme, für die man ggf. erst Kriterien entwickeln muss (oder man checkst sie am Computer)
Hi Reverserk
Ja, richtig. Das Leibniz-Kriterium wäre hier, da es sich um eine alternierende Reihe handelt, das geschickteste.
Du musst also, um bei dieser Reihe Konvergenz nachweisen zu können, feststellen, ob...
- b_k monoton fallend ist
- b_k eine Nullfolge ist.
Trifft beides zu, so ist die Reihe konvergent.
Viel Erfolg
LG
Aus Langeweile schreib' ich's dir gleich mal hin.
Nummer 1: Monoton fallend?
b_k > b_k+1 damit Aussage wahr
1/(5n+1) > 1/(5n+2)
<=> 5n+2 > 5n+1
<=> 1>0
Wahre Aussage
Nummer 2: Nullfolge?
lim{n->inf} b_k
-> lim{n->inf} 1/(5n+1)
Entweder weiß man, dass 1/(5n+1) klar gegen 0 geht, oder man schätzt es mit dem Majorantenkriterium auf 1/n ab, was klarerweise gegen 0 strebt.
Die Folge b_k ist monoton fallend & eine Nullfolge.
Daher ist ihre alternierende Reihe konvergent.
LG
Du hast in der Reihe ein (-1)^(n+2), was sich aufpallten lässt als (-1)^n * (-1)² = (-1)^n
Damit hast du ganz klar alternierendes Vorzeichen.
Der Nennerterm wird für steigende n immer größer daher ist das ganze eine Nullfolge.
Nullfolge mit Alternierende Vorzeichen -> Leibnizkriterium und die Reihe ist konvergent.
Eine allgemeine Methode gibt es dafür allerdings nicht. Das ist von Reihe zu Reihe verschieden und das allgemeinste was sich angeben lässt ist Minoranten- und Majorantenkriterium.
Btw vorsicht wenn steht (-1)^(n*2), denn das ergibt ((-1)^n)² und ist daher für jedes n 1. Eine Reihe wo (-1)^(n*2) davor steht hat also kein alternierendes Vorzeichen.
Jo Majoranten und Minoranten Kriterium kenne ich auch, wie gesagt ich hoffte eigentlich eine Allgemein gültige Methode zu finden die auf alle Reihen anwendbar ist.