Mathegenies da draußen (Funktionen höheren Grades)?
Hallo an alle Mathegenies da draußen!
ich stecke in einer Aufgabe fest und wäre über jegliche Art von Hilfe dankbar!
2. Der Verlauf einer Grippeepidemie in einer Gemeinde kann näherungsweise durch eine ganzrationale Funktion 3. Grades e(t) beschrieben werden.
Dabei gibt e die Anzahl der Erkrankten in Abhängigkeit von der Zeit t in Wochen seit Ausbruch der Epidemie an.
Nach 5 Wochen wurden 66 kranke gemeldet, nach 10 Wochen waren es 172.
Nach 15 Wochen waren es 198 gemeldete Erkrankte.
a) Formulieren die Gleichung der Funktion e(t) für den Verlauf der Grippeepidemie
Das habe ich bereits gelöst : e(t)=-0,16x^3+32x^2+12x
b) Wie viele Menschen erkrankten nach 3 Wochen?
Laut meiner Berechnung sind das 28 Erkrankte (für x=3 eingesetzt)
c) Zu welchen 2 Zeitpunkten sind jeweils 100 Personen erkrankt?
Ich setze für y=100 ein. Und dann?
d) Wann ist die Epidemie beendet?
e) Wann erreicht die Grippeepidemie ihren Höhepunkt?
Über zügige Rückmeldungen würde ich mich sehr freuen! :)
6 Antworten
Deine Funktion ist falsch, setze mal die Werte ein. Runde nicht die Brüche in der Funktion. Du brauchst einen vierten Wert um alle Parameter einer 3-gradigen Funktion (Ansatz: e(t) = a t^3 + b t^2 +c t +d) zu bestimmen. Ist also f(0) = 1 oder f(0) = 0 (ich gehe von =1 aus)?
a) Mit dem Ansatz erhälst du ein lineares Gleichungssystem und als Lösung:
- a= -121/750
- b= 81/25
- c= 5/6
- d= 1
b) Ja, du setzt x=3 ein. e(3) = 28,304
c) Benutze den GTR, sowas per Hand zu rechnen ist unnötig aufwendig. Du hast 3 t-Werte, die die Bedingung erfüllen:
- t= -0,50455
- t= 6,5444
- t= 18,584
Logischerweise entfällt der erste, weil hier die Zeit nicht negativ sein kann.
d) Berechne t aus e(t) = 0, die Funktion ist ab da (bzw. schon vorher) monoton fallend, es gibt keine negative Anzahl Infizierte: t= ca. 20,3514
e) Erste und zweite Ableitung berechnen:
- e'(t) = -(121*t^2)/250 + (162*t)/25+ 5/6
- e''(t)= -(726*x-4860)/750
e'(t) Null setzen und t berechnen (nimm den GTR):
- t= ca 13,5158, e''(t) < 0, also Höhepunkt, gesuchtes t
- t= ca -0,1274, e''(t) > 0 , also Minima, unwichtig.
dankesehr, magst du mir verraten wie genau ich bei c) das ergebnis mit dem taschenrechner herausfinden kann?
a) Formulieren die Gleichung der Funktion e(t) für den Verlauf der Grippeepidemie
Das habe ich bereits gelöst : e(t)=-0,16x^3+32x^2+12x
Da stimmt was nicht. Wenn ich in die Gleichung 5 einsetzen, kom men 840 raus und nicht 66.
1/2 h später:
So, habe die Funktion nachgerechnet und bei mir kommt raus:
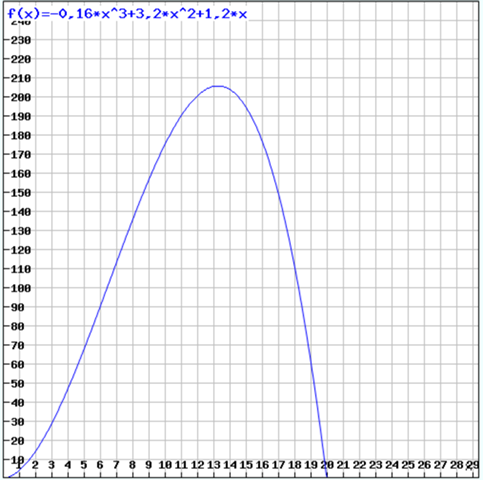
e(t) = -016 t^3 + 3,2 t^2 + 1,2x
Und so sieht die Funktion aus.
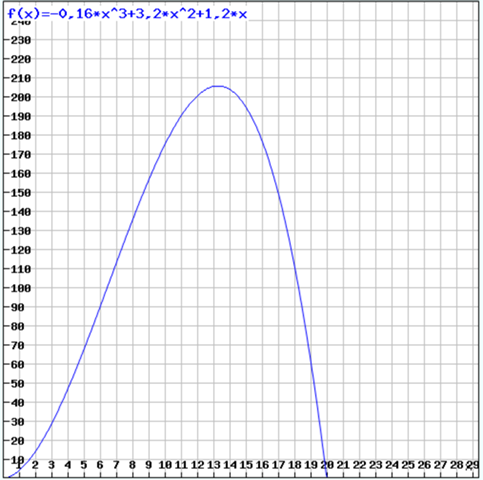
Man kann zunächst sehen, dass die vorgegebenen Werte mit dem Graphen übereinstimmen.
b) Wie viele Menschen erkrankten nach 3 Wochen?
Laut Graph: 28
c) Zu welchen 2 Zeitpunkten sind jeweils 100 Personen erkrankt?
Laut Graph: 6,5 Wochen und 19,2 Wochen
d)nach 20 Wochen
e) nach 13,5 Wochen.
Das weiß ich auch nicht, aber vielleicht hilft es ja schon mal, die richtige Funktion und die richtigen Ergebnisse zu kennen. Für die rechnerische Lösung hatte ich leider keine Zeit mehr.
vielen vielen dank für deine mühen! das hilft mir sehr
genau die formel hatte ich übrigens auch ausgerechnet, allerdings hat gutefrage aus meinen kommas lediglich eine andere schriftart gemacht und sie werden somit garnicht angezeigt...
Ok du musst pq Formel bei a) anwenden
Bei b) musst du cos geteilt durch tan rechnen
bei c) genau dat selbe
bei d) und e) musst du e hoch x berechnen und dann geteilt durch sin
MFg
danke danke und sonst so? was machst du in deiner freizeit außerhalb den stunden, die du damit verbringst unschuldige kleine kinder auf online plattformen zu verklapsen? :)
Ich wollte dir helfen, aber wenn du so giftig reagierst, haste meine Hilfe nicht verdient.
Ich habs gerade noch nicht so ganz durchdacht, aber bei c) könntest du erstmal versuchen, das x auszuklammern, dann hättest du den ersten x-Wert und dann (meine ich) mit dem Rest die pq-Formel anwenden. Negative Ergebnisse fallen weg, weil der Zeitpunkt schlecht negativ sein kann.
Bei e) musst du die erste Ableitung der Funktion bilden, diese gleich Null setzen und nach x auflösen. Danach noch mit der zweiten Ableitung überprüfen, welches Ergebnis ein Hochpunkt ist.
Bei d) bin ich mir grade selbst nicht sicher, aber du kannst versuchen die Nullstellen auszurechnen. Der größte x-Wert dürfte ja dann der Zeitpunkt sein, zu dem die Infektionen wieder bei 0 liegen.
Ich hoffe ich konnte helfen :)
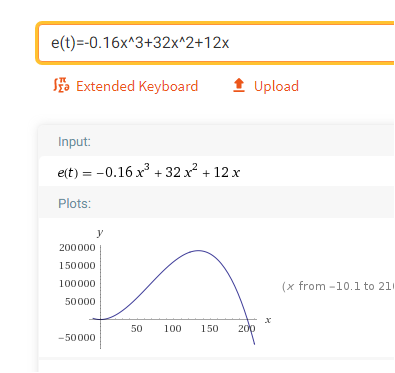
so sieht die Fkt aus
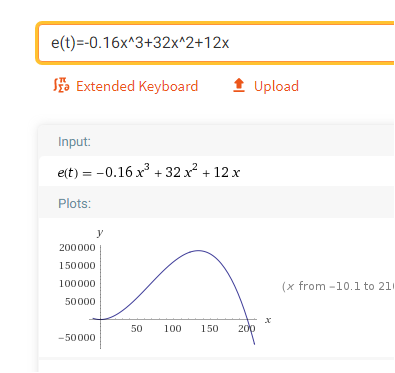
c)
e(t) = 100 setzen und die beiden Werte bestimmen :
e(t)=-0.16 x³ +32 x² +12 x = 100
...
......diese glg krist du nur mit TR raus !
e(t)=-0.16 x³ +32 x² +12 x - 100 = 0
d) Nullstelle berechnen
e(t) = 0
e)
e'(t) bestimmen und gleich Null setzen für den Hochpunkt
vielen dank! das hat schonmal geholfen
allerdings weiß ich nicht, wie ich die gleichung rauskriege mithilfe des taschenrechners... habe ich noch nie zuvor machen müssen.
magst du mir sagen, was ich eingeben muss?
das weiß ich nicht .............vielleicht dürft ihr die Glg ja auch graphisch lösen ..........würde mich wundern , wenn das in der Schule gewünscht ist .
wollen wir nur hoffen ,dass ein komplett graphische Lösung ( wer weiß ? ? ) in der Schule gewünscht ist.