Matheaufgabe wie berechnen?
Aufgabe:
Die Diagonale eines Rechtecks ist 25cm lang. Die eine Rechtecksseite ist 17cm länger als die andere. Welchen Umfang hat das Rechteck?
Lg
6 Antworten
Das berechnet man mit dem Satz des Pythagoras indem man das Rechteck in 2 rechtwinklige Dreiecke unterteilt.
Die große Seite hast du schon mit 25 cm und die Kantenlängen sind dann noch x und x+17.
Der gesamte Umfang des Rechtecks musst du dann noch *2 berechnen (sind ja 2 Dreiecke), lautet also 2x+2x+2*17cm = 4x+34cm.
Die Zahlen kannst du sicherlich auch noch selbst in den Satz des Pythagoras einsetzen.
Du hast folgendes Gleichungssystem:
a und b sind die Seitenlängen des Rechtecks. Alle Werte sind in cm.
Die untere Gleichung kannst du nach a oder b auflösen und in die obere Gleichung einsetzen und a und b berechnen.
Tipp: Es gibt zwei Lösungen, die mit negativen Werten ist natürlich die falsche.
Zur Kontrolle: Richtig ist
Das musst du nur noch in die Formel für den Umfang einsetzen!
eine Seite nenne ich eS...,...die andere Seite aS
Nun ist aS + 17 = eS
Und wegen des Pythagoras gilt
25*25 = (aS + 17)*(aS + 17) + aS*aS
Umfang eines Rechtecks:
U = 2a + 2b
oder
U =2(a + b)
Du benötigst die beiden Seiten a und b um den Umfang berechnen zu können. dummerweise stehen die nicht in der Aufgabe.
Wie andere schon schrieben: Pythagoras.
Eine Skizze dazu:

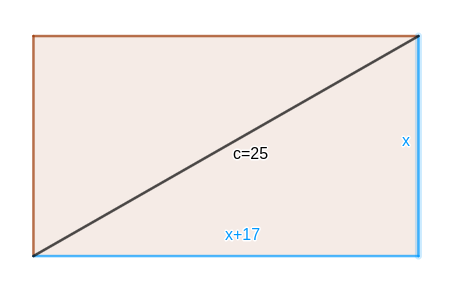
die eine Seite ist x und die andere ist x+17 und nun machst du den Pythagoras mit der Hypotenuse 25 ;
probier mal.