Mathe trigonometrie?

2 Antworten
Der Winkel CAB ist 90° minus gamma.
Die Strecke CD lässt sich aus diesem Winkel mittels Sinussatz berechnen.
Der Winkel CBD ist ebenfalls gleich 90° minus gamma.
Die Strecke DE bekommst du über den Cosinus dieses Winkels.
Nun hast du die gesamte Strecke BD.
Der Abstand lässt sich nun über den Sinus des Winkels ABD berechnen, welcher 90° minus CAB ist.
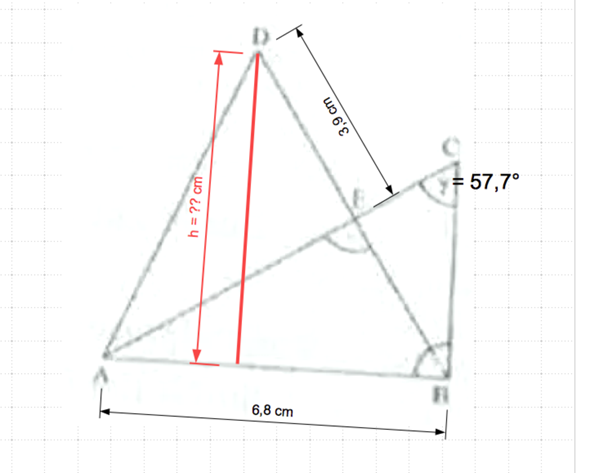
Wenn der Schüler etwas nicht versteht, macht er sich eine Tabelle oder eine Skizze. Hier wäre ein Skizze sehr hilfreich, in die wir die gegebenen und die gesuchten Werte eintragen:

Und nun können wir uns eine Strategie überlegen, die man aber am besten vom gesuchten Ergebnis her anfängt.
Wir stellen fest, der gesuchte Abstand ist die Höhe im Dreick ABD sowie eine Kathede im rechtwinkligen Dreieck FBD, wobei wir den Punkt F als Fußpunkt der Höhe ergänzen.
h können wir daher berechnen, indem wir zuvor die Strecke BD sowie den Winkel ABE ermitteln.
Den Winkel ABE kriegen wir über die Winkelsumme = 180° raus, wenn wir den Winkel CAB = α kennen, der sich leicht ermitteln lässt.
Mit der Strecke AB = 6,8 cm sowie α lässt sich auch die Strecke BE berechnen und dann haben wir alles, was wir brauchen.
Also fangen wir an zu rechnen:
α = 180° - 90° - 57,7° = 32,3°
EB/6,8 cm = sin α
EB = 6,8 cm * sin 32,3° = 3,634 cm
BD = 3,634 cm + 3,9 cm = 7,534 cm
Winkel ABE = β1 = 180° - 90° - 32,3° = 57,7°
h/BD = sin β1
h = BD * sin β1 = 7,534 cm * sin 57,7° = 6,37 cm
Aber bitte nachrechnen!!