Mathe Aufgaben lösen? Dreick?
Hallo Leute, ich muss einen Mathe Aufgabe lösen und komme da einfach nicht weiter. Also ich muss wissen, wie lang der Fluss ist (Aufgabe eins) aber egal wie sehr ich nach einer Antwort suche, ich finde keine. Bitte um Hilfe. Danke.
4 Antworten
wo fängt der Strahlensatz an ( bildlich gesprochen )
bei S
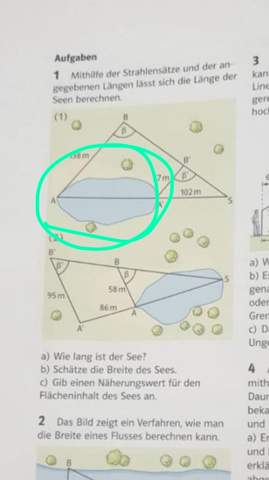
die 7m verhalten sich zu den 138m wie 102 zu 102+x (SA)
als Gleichung ist das
7/138 = 102/(102+x)
innenprodukt = außenprodukt
138*102 = 7*(102+x)
138*102 = 7*102 + 7x
( (138*102) - 7*102 ) / 7 = x = ca 1908.86
wirkt viel , aber testen kann man es
7 zu 138 = 19.71 mal so lang
102+1908.86 = 2010.86
und das ist auch ca 19.71 * 102
andere , nächste
Strahlensatz geht von S aus
SA / SA' = 58/95
jetzt du !
schätze die Breite des Sees?
ich seh da ca die Hälfte
dann ist das ungefähr ein Rechteck um die runden , fehlenden Ecken vermindert ( ca 10 ? 15 ? 20 % )
echt frech so was !
Hallo Frageed!
Das Dreieck ABS ist dem Deieck A'B'S ähnlich, das heißt die Relationen sind gleich.
Die Strecke AB verhält sich zur Strecke A'B', wie die Strecke AS zu A'S. Du kannst also einfach einen Dreisatz machen.
AS = A'S * AB : A'B'
Die gesuchte Strecke ist dann natürlich AS - A'S.
Gruß Friedemann
Die gesuchte Strecke, also Länge des Sees sei x.
Aufgabe 1
Nach dem 2. Strahlensatz gilt:
57 m / 138 m = 102 m / ( x+ 102 m)
Das lösen wir aus:
mal ( x+ 102 m)
( x+ 102 m) * 57 m / 138 m = 102 m
ausklammern und mal 138 m:
x * 57 m + 57m * 102 m = 102 m * 138 m
ausrechnen:
x * 57 m + 5814 m^2 = 14076 m^2
x * 57 m = 8267 m^2
x = 145 m
Abschätzung der Fläche:
Länge l des Sees am Bildschirm gemessen: 12,5 cm
Durchschnittliche Breite b am Bildschirm gemessen: ca. 5cm
Damit gilt:
b / l = 5 cm / 12,5 cm
b = 5/12,5 * 145 m = 58 m
Fläche eines Rechtecks:
A = l * b = 145 m * 58 m = 8410 m^2
Da der See aber kein echtes Rechteck ist, sondern an den runden Seiten etwas Fläche fehlt, runden wir ab und sagen:
Der See hat eine Fläche von ungefähr 8000 m^2
7:102=die zahl die ich nicht sehen kann, weil du sie übermalt hast : (x+102)
x ist die flussbreite, nach x auflösen
also
7:102 = 138? :(102+x)
ja, das ist bei strahlensätzen so, sind immer gleichungen
x:y=a:b
so in der art ist das immer
Also ist das eine gleichungsaufgabe?