Mathe aufgabe zu kompliziert?
Hey,
schreibe in öaar tagen eine mathe arbeit über pythagoras und es läuft eigentlich beim üben ganz gut..dennich habe ich mich bei der folgenden aufgabe gefragt,ob man wirklich den satz des pythagoras verwenden muss oder,ob es nicht viel einfacher geht:
Beim Echoloten sendet man Schallwellen mit einem Sender S zum Meeresgrund und empfängt die reflektierten Wellen mit einem Empfänger E. Je tiefer das Meer ist, desto länger dauert es, bis die Schallwellen zurückkehren. Sender und Empfänger befinden sich 1 m unter dem Wasserspiegel am Schiffsrumpf und sind 10m voneinan-der entfernt. Im Wasser legt der Schall 1,5 km pro Sekunde zurück. An einer bestimmten Stelle benötigt der Schall für den Weg vom Schiff zum Meeresboden und 1 wieder zurück zum Schiff Sekunde. 10 Bestimme wie tief an dieser Stelle das Meer ist.
Also,ich habe es jetzt so asgerechnet:
->der schall legt 1,5km pro sekunde zurück
(Erstmal hab ich dies in meter umgerechnet,also 1500)
->jetzt steht da ja das der weg von sender bis meeresboden zurück zu empfänger 1/10 sekunde gefauert hat..das habe ich dann durch zwei geteilt,also 1/20,weil 1/10 ja die angave für beide hin und zurück war.Und folgend hab ich einfach die 1500 durch 20 geteilt,das ergab dann 75 meter genau.
Stimmt das?wenn ja dürfte man das so machen?
Vielen Dank im Vorraus euch allen^^
2 Antworten
dennich habe ich mich bei der folgenden aufgabe gefragt,ob man wirklich den satz des pythagoras verwenden muss
Wie so oft und gefühlt das dreihundertvierundneunzigste Mal: "Wenn der Schüler etwas nicht versteht, macht er sich eine Skizze oder eine Tabelle".
Skizze:

b + c ist die Laufstrecke des Schalls, b ist die Wassertiefe und a sind 10 m. b und c sind aber nicht gleich lang. Nun musst du b ausrechnen und dabei hilft der alte Pythagoras durchaus.
Man kann natürlich auch so rechnen:

b = c = 75 m
h^2 + 5^2 = 75^2
h = √75^2 - 5^2 = 74,8 m
Wassertiefe t = h + 1 m = 75,8 m
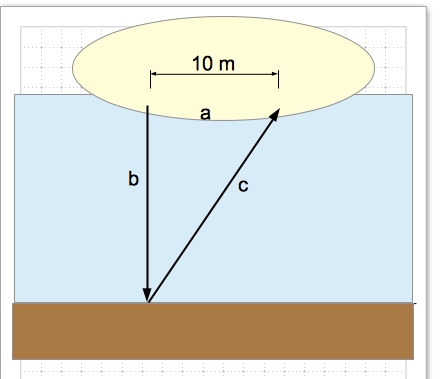
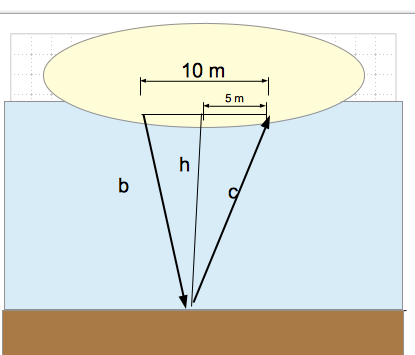
Nun ist ja angegeben, dass Sender und Empfänger 10m voneinander entfernt sind. Nach Reflexionsgesetz ist Einfallswinkel gleich Reflexionswinkel. Es ergibt sich also ein gleichschenkliges Dreieck. Der Einfluss auf das Ergebnis dürfte jedoch marginal sein.
Und vergiss nicht, den einen Meter zu addieren, den die Sensoren unter Wasser sind.