Mathe - wie sieht dieser Graph von f aus?
f' hat einen Wendepunkt im Ursprung und genau einen Hoch und Tiefpunkt
Wie sieht f aus
Ungefähr?
Lg
1 Antwort
Von gutefrage auf Grund seines Wissens auf einem Fachgebiet ausgezeichneter Nutzer
Mathematik
Beschrieben wird die Funktionsschar f'(x) = x³ + ax² + bx mit b ≠ 0.
Eine mögliche Funktion, die den Vorgaben entspräche, wäre beispielsweise:
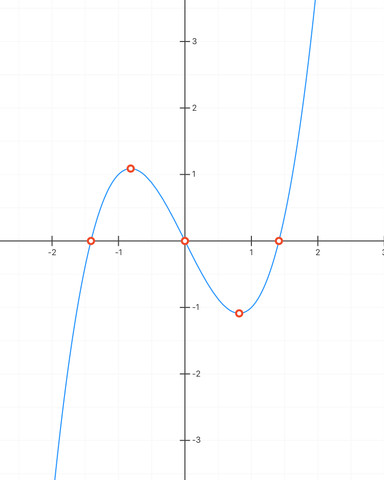
g'(x) = x³ - 2x (a = 0, b = 2).
Ihr Schaubild findest Du im Anhang. Der Graph muss nicht punktsymmetrisch sein, falls das Glied ax² dazukommt, also a ≠ 0 ist, unterscheiden sich die beiden Äste.
Der ungefähre Verlauf ist jedoch bei allen Funktionen dieser Art gleich.
Für f müsste man dann integrieren und kommt auf:
f(x) = 1/4 x⁴ + a/3 x³ + b/2 x² + k
Bei unserer Funktion wäre das:
g(x) = 1/4 x⁴ - x² + k
k ist eine beliebige reelle Zahl.
LG