Komplexe Zahlen Re (z) = 0 Aufgabentyp lösen?
Guten Tag,
ich wollte fragen wie man den folgenden Aufgabentyp lösen kann
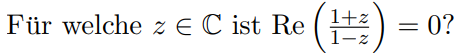
Das Ergebnis sollte in der Form z = x + yi angegeben werden und man muss geeignete Bedingungen an x und y stellen.
Zudem habe ich den Typ die Formel des Betrages mir anzusehen
Ich habe mir gedacht das z für x + yi zu ersetzen und das x für 0 zu ersetzen, da der Realteil ja null sein soll. Nun habe ich (1+yi/1-yi) = 0 stehen. Muss ich dies nun einfach nach b auflösen um die Lösung zu erhalten oder habe ich von Anfang an einen Fehler?
Ich würde mich über Hilfe freuen!
3 Antworten
Du hast da einen kleinen Denkfehler drin: Nicht der Realteil von z soll 0 sein, sondern der Realteil des Bruchs z+1/z-1.
Ich würde da folgendermaßen rangehen:
Setz für z = x + iy ein, Form den Bruch in die Normalform um und setz dann den Realteil = 0.
ich habe nun (1-x²-2xyi+y²)/(1-2x+x²+y²) nach der Erweiterung mit dem komplex konjugiertem erhalten. Soll ich nun in dieser Form die 0 einsetzen oder übersehe ich ein schritt wie man das noch weiter vereinfachen kann?
Das kannst du wieder in die Normalform bringen. Also dass da steht a +ib (a und b sind Terme, die von x und y abhängen). Und davon setzt du den Realteil ("a") = 0. Also nicht 0 einsetzen, sondern gleich 0 setzen.
(1-x²+y²)/(1-2x+x²+y²) - (2xyi)/(1-2x+x²+y²) so in etwas?
Habe das nicht nachgerechnet, aber das sieht gut aus. Und da hast du jetzt ja wieder einen Realteil und einen Imaginärteil und jetzt musst du (nur) noch herausfinden, wann ersterer gleich Null ist.
ah also den ersten Bruch einfach nullsetzen danke!
hm also das einzige was ich bis jetzt habe ist dass: (1-(Betrag Z)²)/(1-2x+(Betrag Z)²) oder ist das der falsche ansatz?
Du setzt ja einen Bruch gleich null. Da reicht es, wenn du den Zähler nullsetzt (und dann sichergehst, dass der Nenner nicht gleichzeitig null ist). Das sollte die Rechnung etwas einfacher machen
Ich habe mir gedacht das z für x + yi zu ersetzen und das x für 0 zu ersetzen, da der Realteil ja null sein soll.
Nein so funktioniert das nicht. (z=-1 erfüllt zum Beispiel die Gleichung)
Setzte zuerst z=x+yi in den Bruch ein.
Erweitere dann den Bruch so, sodass der Nenner reell ist. Spalte den Bruch dann in Real- und Imaginärteil auf. (Also Summand ohne i und Summand mit i als Faktor)
Setzte dann den Realteil gleich 0.
Du erweiterst den Bruch um das Komplex Konjugierte des nenners, korrekt
(1-x²+y²)/(1-2x+x²+y²) - (2xyi)/(1-2x+x²+y²) so in etwa?
Da x=0 ist bist du schon auf der richtigen Fährte. Allerdings, wo ist da ein b?
sorry hab das b mit dem y verwechselt^^ es gibt ja die a+ib und x+iy schreibweise
also den Bruch (1+(x+iy))/(1-(x+iy)) umformen?