Könnt ihr mir bitte helfen. Danke?
Ich finde leider keine Videos dazu, wie ich den Grenzverhalten anhand Abbildung bestimme. Könnt ihr mir das bitte erklären anhand dieser Aufgaben. Schreibe nöchste Woche Klausur, bitte hilft mir. Wäre sehr dankbar dafür danke

2 Antworten
fangen wir mal mit Aufgabe a) an:
Zunächst betrachten wir den Defintionsbereich. Der geht offensichtlich von -∞ bis +∞ mit Ausnahme von x = -3. Mathematisch formuliert man das z.B. so:

Bei -3 wird der Nenner der gebrochen rationalen Funktion zu 0. Durch 0 teilen darf man aber nicht. Wir haben also 3 Werte, die wir betrachten müssen. Das ist +∞, -∞ und -3.
Fall 1: x geht gegen minus unendlich. Dann nähert sich y, also der Funktiosnwert, der 3 an. Das schreiben wir so:

Fall 2: x geht gegen plus unendlich. Dann nähert sich y, also der Funktiosnwert, der 3 an. Das schreiben wir so:

Fall 3: x geht gegen -3. Da haben wir aber unterschiedliche Grenzwerte, ob wir uns von links oder rechts der -3 nähern. Daher müssen wir eine Fallunterscheidung durchführen.
Zuerst der rechtsseitige Grenzwert, wenn wir und also von rechts der Polstelle nähern. Dann geht f(x) gegen minus unendlich. Da gibt es verschiedene Schreibweisen. Eure kenne ich nicht. Es könnte aber so aussehen:

Nun der linksseitige Grenzwert, wenn wir und also von links der Polstelle nähern. Dann geht f(x) gegen plus unendlich:

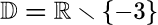

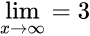
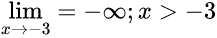
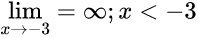
kann doch sehen
a)
lim gegen + und - unend ::::: +3
(weil x/x+2 zur 1 wird und dann +2)
.
lim gegen -2
von links +
von rechts - unend
.
b) sollte nun kein Problem mehr sein. kein f(x) zu sehen , aber da sollte ein +0.5 dabei