Kirmes Aufgabe stochastik?
Ich weiß das ich den durchschnittliche Gewinn ausrechnen muss, aber wie mache ich das beim 1. und beim 3.?
3 Antworten
Du musst den Erwartungswert berechnen, und schauen das der Erwartungswert nicht kleiner null ist:
1.) Aufgabe:
Erwartungswert = 1/6 * (-1) + 1/6 * (-2) 1/6 * (-3) 1/6 * (-4) 1/6 * (-5) 1/6 * (-6) = -3€ pro Spiel
3.) Aufgabe:
Erwartungswert = 3/16 * 1 + 9/16 *4 = ca. 2,44€
Es steht da aber auch auch in Dick dass die Augensumme betrachtet wird
ja aber es könnten auch 5 Würfel sein und die Graphik alleine ist meiner Meinung nicht aussagekräftig genug
Dann hätte man auch 5 Würfel gezeichnet, bei dem 2. Ist ja auch klar wie der Versuch abläuft. Das einzig blöde ist das dritte, da da überhaupt nichts steht
Die Würfeln könnten meiner Meinung auch rein symbolischer Natur sein.
Bei der zweiten Aufgabe wird ganz genau ein Tortendiagramm dargestellt (das ist eine weltweit anerkannte Methode um einen Bruch genau darzustellen).
Und bei der dritten gebe ich dir Recht da kann man nur spekulieren.
Nur um sicher zu gehen wäre das bei zwei dann
1/4*1 +3/4*0?
ja genau und ich muss noch betonen das ich bei der 1. Aufgabe mir nicht sicher war wie viele Würfeln im Spiel sind und habe deshalb pauschal nur mit einem gerechnet.
Wenn es zwei Würfel wäre, was würde sich ändern?
du hättest 36 verschiedene Würfelpaare als 6*6 und jedes Würfelpaar hätte die Wahrscheinlichkeit von 1/36
Ich wäre ihnen sehr verbunden wenn sie mir das einmal vorrechnen können, gerade Check ich es nicht.
Würfelpaar (1,1) = 1/36 * ((1+1) - 7) = ca. -0,14€ => diese musst du mal zwei rechnen da es diesen Würfelpaar doppelt gibt.
könnte ich nicht auch einfach den alten erwartungswert nehmen nur mit 1/36 austauschen und dann mal 2 nehmen ?
Ich glaube das wird nicht helfen du hast alleine schon 6 verschiedene Paare wenn eines davon eine 1 ist(also ohne doppelten Paaren):
(1,1) = 1/36 * (-5)
(1,2) = 1/36 * (-4)
(1,3) = 1/36 * (-3)
(1,4) = 1/36 * (-2)
(1,5) = 1/36 * (-1)
(1,6) = 1/36 * 0
(1,1) kommt nur ein Mal vor, hat also die Wahrschlichkeit 1/36
Ich bin irgendwie gerade zu doof dafür, Stochastik ist so lange her bei uns
Den durchschnittliche Gewinn nennt man Erwartungswert, denn das ist der Wert, denn du bei vielem mal Spielen auf langer Sicht erwartest.
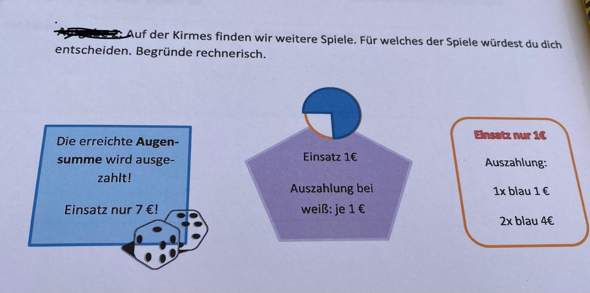
Erstes Spiel: Hier würfelst du zwei Würfel gleichzeitig und ihre Augensumme ist der Betrag, den du ausbezahlt bekommst. Für jedes Mal würfeln musst du aber 7 Euro zahlen. Die verschiedenen Augensummen, die möglich sind, lauten: 2 (1 und 1), 3 (2 und 1), 4 (2 und 2), 5 (2 und 3), 6 (1 und 5 oder 3 und 3 oder 4 und 2), 7 (4 und 3 oder 6 und 1 oder 5 und 2) 8 (5 und 3 oder 4 und 4), 9 (6 und 3 oder 5 und 4), 10 (5 und 5), 11 (5 und 6), 12 (6 und 6). Und natürlich weil es zwei Würfel gibt, gibt es jeweils 2 Möglichkeiten für die unterschiedlichen Möglichkeiten, die ich genannt habe.
Ich habe dir die Tabelle für das erste Spiel gemacht (so eine Tabelle solltest du für jedes Spiel machen):

Den Erwartungswert für dieses Spiel berechnest du nun, indem du jeweils immer px absolut mit dem dazugehörigen (direkt darunter) px in Prozent multiplizierst und diese dann addierst, also so: 2 * 0.0625 + 2* 0.0625 + 2* 0.0625 + 2*0.0625 + 6*0.0625 etc.
So eine Tabelle machst du nun für alle 3 Spiele und dann berechnest du den Erwartungswert (die Tabelle für das erste Spiel habe ich die Tabelle ja schon für dich gemacht, du musst nur den Erwartungswert noch berechnen).
Und dann hast du 3 Erwartungswerte. Dort, bei dem der Erwartungswert = 0 ist, ist das Spiel, welches fair ist. Und wenn bei keinem der Erwartungswert 0 ist, dann hätte ich, das Spiel genommen, dessen Erwartungswert entweder positiv und/oder am nächsten zu 0 ist.
Sorry!!
Ich habs falsch gemacht, du musst die Zahlen noch -7 rechnen. Die möglichen Gewinne sind anstatt 2-12 "die Zahlen -5, -4, -3, -2, -1, 0, 1, 2, 3, 4 und 5". Ich habe vergessen, dass du ja 7 Euro zuerst bezahlen musst.

Es ist egal, ob du erst den Einsatz abziehst und dann den erwartungswert bildest oder anderes Rum.
Außerdem passen deine Werte für die Absoluten Wahrscheinlichkeiten nicht, da es insgesamt 36 mögliche Ereignisse sein sollen und es z.b für die 2 nur eine Möglichkeit (1,1) gibt.
Man sollte außerdem das Spiel nehmen, dessen erwartungswert am größten ist, da man da mehr Gewinn erwarten würde, ein faires Spiel bedeutet nur, dass beide Seiten keinen Gewinn erwarten werden.
Können sie mir vielleicht den Erwartungswert berechnen, ich versuche es jetzt schon länger, aber irgendwie will es einfach nicht :(
Die möglichen Würfelsummen mit deren Wahrscheinlichkeiten sind:
2 - 1/36
3 - 2/36
4 - 3/36
5 - 4/36
6 - 5/36
7 - 6/36
8 - 5/36
9 - 4/36
10 - 3/36
11 - 2/36
12 - 1/36
Jetzt rechnest du jeweils Gewinn * Wahrscheinlichkeit und addierst dann alles zusammen, am Ende ziehst du 7 ab
Also ist dann das dritte Spiel am besten oder ? Weil das ist der Erwartungswert ja 2,44
1) Du musst den Erwartungswert der Summe zweier Würfel bestimmen und davon 7 abziehen.
Da die beiden Würfel unabhängig voneinander sind, ist der Erwartungswert der Summe gleich zwei Mal dem erwartungswert von einem Würfel. (Falls ihr das nicht hattet, musst du das wohl mühsam per Hand ausrechnen)
3)
Hier steht nicht was genau gemacht wird (kann auch sein dass es abgeschnitten wurde)
Ich vermute Mal dass das Rad zwei Mal gedreht wird.
Bestimme die Wahrschlichkeit dass zwei Mal blau gedreht wird und rechne das Mal 4€, das selbe machst du mit ein Mal Blau (dann Mal 1€) das addierst du dann zusammen und ziehst dann 1€ ab
solche graphischen Andeutungen wie bei der ersten Aufgabe mit den zwei Würfel finde ich in einem Mathematik Studium sehr fragwürdig, da diese Graphik auch rein symbolischer Natur sein kann.
Solche Informationen gehören ordentlich deklariert.