Kann mir jemand bei dieser Chemie-Aufgabe zur Konzentrationsberechnung helfen?
Hallo,
wir haben in Chemie diese Aufgabe zur Berechnung der Konzentration in einer galvanischen Zelle bekommen. Weiß jemand vielleicht, wie genau man das machen soll? Die Beispielaufgabe war nämlich etwas leichter. Als Formeln haben wir:
E= E^0+0,059V/z •lg(Ox)
und für die Zellspannung
U = E (Akzeptor)- E(Donator)
Bzw vereinfacht:
U = 0,059V/z • lg(Red/Ox)
Bin sehr dankbar für jeden Ansatz und für jede Hilfe! 🙏 Komme nämlich einfach nicht weiter.
Danke im Voraus!

ganz vergessen: die Konzentration in der Nickelzelle ist c= 0,1mol/l und E^0(Ni/Ni2+) = -0.23V; E^0(Cr/Cr3+) = -0,74 V.
3 Antworten
Ich fasse Deine Angabe zusammen:
- Du hast zwei Elektroden:
- Einerseits eine Nickelelektrode ε⁰(Ni²⁺/Ni)=−0.23 V und c(Ni²⁺)=0.1 mol/l
- Andererseits eine Chromelektrode unbekannter Konzentration, ε⁰(Cr³⁺/Cr)=−0.74 V
- Die Chromelektrode ist negativ, also werden dort Elektronen abgegeben, also findet eine Oxidation statt.
- Die Reaktion lautet also 3 Ni²⁺ + 2 Cr ⟶ 3 Ni + 2 Cr³⁺
- Man mißt ΔE=0.6575 V Spannung zwischen den Elektroden.
Ich habe aus drei Gründen Bauchschmerzen. Einer davon hängt damit zusammen, daß ich hier in Marokko irgendwelche hartnäckigen Bakterien inkorporiert habe und seit 1½ Wochen darunter leide, aber das hat nichts mit dem Beispiel zu tun. Die anderen beiden sind aber relevant.
Erstens bin ich mir überhaupt nicht sicher, ob bei dieser Reaktion wirklich Cr³⁺ und nicht nur Cr²⁺ entsteht. In Säuren löst sich metallisches Chrom nur zu Cr²⁺, und H₃O⁺ ist ein stärkeres Oxidationsmittel als Ni²⁺. Andererseits ist das nur ein kinetischer Effekt, und vielleicht ist er für Deine Reaktionsbedingungen nicht relevant.
Zweitens stört mich, daß das ε⁰ für beide Metalle nur auf zwei Nachkommastellen gegeben ist. Meine Quelle (Holleman–Wiberg) sagt übrigens ε⁰(Cr³⁺/Cr)=−0.744 V und ε⁰(Ni²⁺/Ni)=−0.257 V, und letztere Zahl (die sich auch bei Wikipedia findet) widerspricht Deinen Angaben.
Hier das Chromdiagramm aus dem Holleman–Wiberg:

Selbst meine Zahlen (mit denen ich im folgenden weiterrechnen werde) sind nur auf drei Stellen genau, und Deine vierstellige Angabe für das gemessene Potential wirkt auf mich wie ein Zufallszahlengenerator. Ich habe den Verdacht, daß Deine Angaben nicht aus der Praxis kommen (wo man wohl irgendeine Art von Eichung machen würde), sondern daß sich das jemand im Lehnstuhl aus dem Stammhirn zusammengepfriemelt hat. Im folgenden rechne ich mit meinen Zahlen für die Potentiale weiter.
Nachdem ich meine Bauchschmerzen ausführlich erläutert habe, rechnen wir das Beispiel einfach durch. Da wir die Reaktionsgleichung bereits haben, können wir sofort die Nernst-Gleichung dazu anschreiben und nach der gewünschten Variable c(Cr³⁺) auflösen. Die Zahl der ausgetauschten Elektronen ist natürlich z=6, und ΔE⁰ = ε⁰(Ni²⁺/Ni) − ε⁰(Cr³⁺/Cr) = +0.487 V
3 Ni²⁺ + 2 Cr ⟶ 3 Ni + 2 Cr³⁺

Wir kriegen also eine sehr kleine Chromkonzentration, was zu erwarten ist, weil sich das gemessene ΔE deutlich vom ΔE⁰ unterscheidet. Mit Deinem zweifelhaften Wert für das ΔE⁰ würde man deutlich größere Werte in der Gegend von ≈10¯⁹ mol/l bekommen.
Abschließend noch eine Bemerkung zur Antwort von suplol: Die dort gezeigte Vorgangsweise ist valide. Ich habe die Nernst-Gleichung auf die ganze Reaktion angewendet, er hat sie separat für die beiden Halbzellen formuliert. Es sollte also dasselbe herauskommen, aber das tut es nicht, weil er für das Nickel- und Chrompotential die Werte −0.76 und −0.236 V recherchiert hat (zur Erinnerung: Die Zahlen in Deiner Angabe sind −0.74 und −0.23 V, die Zahlen mit denen ich gerechnet habe sind −0.744 und −0.257 V). In diesem Zahlenchaos hat er sich verschustert und dann unverständlicherweise mit den gemischten Werten ε⁰(Ni²⁺/Ni)=0.76 V und ε⁰(Cr³⁺/Cr)=0.23 V weitergerechnet. Es hat mich eine gute halbe Stunde gekostet, herauszufinden, woher die Diskrepanz von immerhin einer Zehnerpotenz in der Cr³⁺-Konzentration herkommt.
Daraus kann man einige Lehren ziehen:
- Es ist essentiell, daß man sagt, mit welchen Zahlen man rechnet; das aus der numerischen Wüste wieder zurückzurechnen, ist sehr zeitaufwendig.
- Mit Zahlen herumzujonglieren, ist fehleranfällig; deshalb empfehle ich allen, es so zu machen wie ich: Man rechnet das abstrakt durch und setzt die Zahlen erst am Ende ein. Als Bonus kann man in die Endformel auch verschiedene ε⁰-Werte einsetzen und nachprüfen, wie stark sich das aufs Ergebnis auswirkt.
- Und dabei bemerkt man etwas ganz Wichtiges: In diesen Rechnungen reagieren die berechneten Konzentrationen extrem empfindlich auf die numerischen Werte der Standardpotentiale; in unserem Beispiel haben 0.02 V Unterschied im ε⁰(Ni²⁺/Ni) bei suplol die Chromkonzentration verzehnfacht. Ich habe Dich bereits am am Anfang dieser Antwort (als die Antwort von suplol noch gar nicht veröffentlicht war) darauf hingewiesen, daß ich die zweistellige Genauigkeit der ε⁰-Werte und die vierstellige Genauigkeit des ΔE für fischig halte, und ich wurde voll bestätigt. Hier muß man eine anständige Eichkurve machen und kann keine Tabellenwerte für die ε⁰ verwenden, wenn man die Konzentrationen verläßlich bestimmen will.
Damit Du in diesem Chaos verschiedener Resultate nicht komplett den Faden verlierst, setzen wir übungshalber die verschiedene Werte in die Endformel ein:

- ε⁰(Cr³⁺/Cr)=−0.74 V und ε⁰(Ni²⁺/Ni)=−0.23 V (deine Angabe) ⟹ c(Cr³⁺)=1.05 nmol/l
- ε⁰(Cr³⁺/Cr)=−0.76 V und ε⁰(Ni²⁺/Ni)=−0.23 V (Rechnung von suplol) ⟹ c(Cr³⁺)=11 nmol/l
- ε⁰(Cr³⁺/Cr)=−0.76 V und ε⁰(Ni²⁺/Ni)=−0.236 V (deutsche Wikipedia, zitiert von suplol) ⟹ c(Cr³⁺)=5.4 nmol/l
- ε⁰(Cr³⁺/Cr)=−0.744 V und ε⁰(Ni²⁺/Ni)=−0.257 V (aus dem Holleman–Wiberg, 103. Auflage, 2017, derselbe Wert für Nickel steht auf der englischen Wikipedia, die leider kein Chrompotential angibt) ⟹ c(Cr³⁺)=0.071 nmol/l
Du siehst, das sind die reinsten Hausnummern.

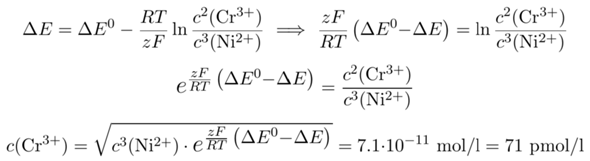
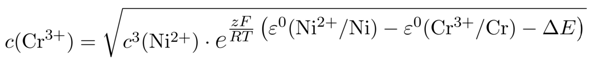
Zellspannung berechnen:
U=E0(Akzeptor)−E0(Donator)U = E^0(\text{Akzeptor}) - E^0(\text{Donator})U=E0(Akzeptor)−E0(Donator)
- Nernst-Gleichung nutzen:
U=U0−0,059z⋅log(RedOx)U = U^0 - \frac{0,059}{z} \cdot \log\left(\frac{\text{Red}}{\text{Ox}}\right)U=U0−z0,059⋅log(OxRed)
- Konzentration berechnen:
log(RedOx)=U0−U0,059/z\log\left(\frac{\text{Red}}{\text{Ox}}\right) = \frac{U^0 - U}{0,059 / z}log(OxRed)=0,059/zU0−U
Danach:
RedOx=10Ergebnis\frac{\text{Red}}{\text{Ox}} = 10^{\text{Ergebnis}}OxRed=10Ergebnis
Setze Werte ein und löse nach der gesuchten Konzentration (Ox\text{Ox}Ox oder Red\text{Red}Red) auf!
Bestimme bei solchen Aufgaben immer zuerst mal die Reaktionsgleichungen oder entnimm sie der elektrochemischen Spannungsreihe:


Hier sehen wir, dass Nickel ein weniger negatives (im Vergleich zur Standardwasserstoffelektrode) Potential als Chrom hat und daher reduziert wird.
Das stimmt mit der Information, dass die Chromhalbzelle den Minuspol bildet, überein.
Mit der Nernstgleichung berechnest du das Potential einer Halbzelle.
Für die Nickel-Halbzelle ergibt das:
E = E° + 0,0295V * log[Ox]/[Red] = E° + 0,0295V * log[Ni2+] = -0,2595V
Die Zellspannung
ΔE = E(Kathode) - E(Anode) = E(Nickel-Halbzelle) - E(Chrom-Halbzelle) = 0,6575V
Umgeformt ergibt:
E(Chrom-Halbzelle) = -0,2595V - 0,6575V = -0,917V
Nernst für Chrom-Halbzelle:
-0,917V = -0,76V + 0,059V / 3 * log[Cr3+]
log[Cr3+] = -0,157V * 3/ 0,059V ≈ -8
[Cr3+] = 10-8 M
Bemerkung: Bei beiden Halbzellen vereinfacht sich log[Ox]/[Red] zu log[Ox], da sowohl Ni, als auch Cr eine Aktivität von 1 haben


Ich habe einfach die von Wikipedia genommen: https://de.wikipedia.org/wiki/Elektrochemische_Spannungsreihe#Elektrochemische_Spannungsreihe
Zusätzlich ist mir dann ja noch der Fehler unterlaufen mit E°(Ni2+) = -0,23V zu rechnen, statt mit -0,236V. Was ja am Ende schon einen enormen Unterschied macht
Ja, ein satter Faktor 2 nur für diese winzige Änderung, und ein Faktor 10 für den Wechsel zwischen 0.76 und 0.74 fürs Nickel. Diese Aufgabe hat einfach eine perverse Fehlerfortpflanzung.
Du hast mich eine halbe Stunde meines Lebens gekostet, in der ich herumgerechnet habe, um zu verstehen, warum Deine Antwort von meiner um einen Faktor 150 abweicht. Antwort: Andere Standardreduktionspotentiale. ☹