Java Ellipse aus Linien zeichnen - Fehler wegen nur ganzzahlig möglichen Winkeln?
Hallo,
ich möchte in Java einen Farbkreis in Form eines Ellipse zeichnen; dafür zeichne ich Linien verschiedener Farben vom Mittelpunkt aus in einem bestimmten Winkel zum Endpunkt, der auf der imaginären Form einer Ellipse liegt. So weit so gut, das funktioniert auch.
Mein Problem allerdings ist, dass die Farbkreis-Ellipse nach dem Zeichnen ganz und gar nicht so aussieht, wie sie aussehen sollte:
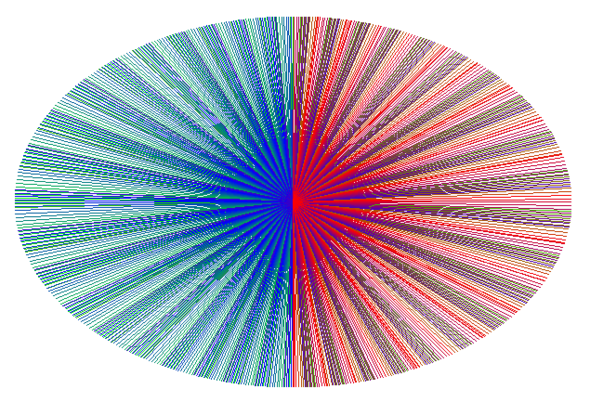
Ich vermute, dass es daran liegt, dass die Berechnungen Gleitkommazahlen ergeben, die ich aber ganzzahlig runden muss, damit ich damit das Ende einer Linie als Punkt kennzeichnen kann. Dadurch liegen die Linien womöglich an manchen Stellen aufeinander und an anderen Stellen existieren keine Linien (ist das so?).
Hier der Code zum Definieren der Linien mit Farbe und Index:
Line[] lines = new Line[3*255];
int[] color = {255,0,0};
for(int i=0; i<3; i++)
for(int j=0; j<255; j++){
color[i]--; color[(i+1)%3]++;
lines[i*255 + j] = new Line(i*255 + j + 1, new Color(color[0], color[1], color[2]));
}
Zeichne ich die Linien mit aufsteigender Länge nebeneinander, funktioniert der Farbübergang so wie geplant - nur die Farbellipse macht Probleme.
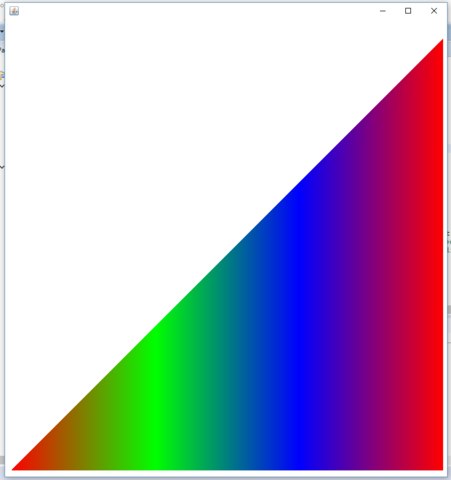
Hier der Konstruktor der Line-Klasse (mehr enthält sie mom. noch nicht):
Line(int index, Color color){
this.index = index;
this.color = color;
this.angle = this.index*360./765; //3*255 Farben
int a = Ellipse.a, b = Ellipse.b;
double x = (a*b/Math.sqrt(b*b+Math.pow(a*Math.tan(angle), 2))),
y = x*Math.tan(angle);
if(angle > 90 && angle < 270) x = -x;
this.end = new Point((int) x, (int) y);
this.length = Point.distance(0, 0, end.x, end.y);
}
Die paint-Methode der Frame Klasse (ja, ich programmiere in Swing, die Ellipse ist eher ein quick&dirty-Projekt):
@Override public void paint(Graphics g){
for(int i=0; i<3*255; i++){
g.setColor(lines[i].color);
g.drawLine(m.x, m.y, lines[i].end.x+m.x, lines[i].end.y+m.y);
}
}
Warum sieht die gezeichnete Ellipse so grausam im Gegensatz zum Dreieck aus und separiert optisch so stark zwischen rot und blau? Woran liegt das bzw. wie kann ich es beheben?
Vielen Dank schon mal im Voraus.
LG
5 Antworten
Hallo Willibergi,
ganz "schönes" Problem. Der Grund ist, wie Du ja selbst schon anmerkst, dass Du runden musst. Du bist schließlich an die Auflösung gebunden.
Beheben könntest Du das Problem indem Du auf einem wesentlich größeren Grafik-Kontext zeichnest und diesen dann, sobald er fertig gerendert ist runter-skalierst auf deine Auflösung. Da müsstest Du womöglich ausrechnen, wie groß der Grafikkontext sein muss, damit Du keine Lücken erzeugst.
Eine andere Möglichkeit wäre die Logik umzudrehen. Also nicht Linien zu zeichnen, sondern zu jeder Koordinate x,y die Farbe zu berechnen und dann genau den Punkt mit der Farbe zu zeichnen. So überspringst Du natürlich keine Punkte.
Gruß
Du würdest im zweiten Schritt ja verkleinern. Von außen nach innen zeichnen halte ich auch für interessant.
Ich probiere grad mal verschiedene Lösungen aus.
Gruß
So wie ich den Code verstehe iterierst Du über die falsche Größe.
Im Endeffekt möchtest Du über die Koordinaten, die Integralwerte sind, iterieren.
Ich meine die Logik, Du iterierst doch über die Farben und erzeugst eine Linie je Farbe, wobei Du je Linie einen Endpunkt auf der Ellipsenlinie berechnest.
Möchtest du aber eine vollständige Ellipse, dann mußt Du über die Koordinaten iterieren, also z.B. über x und den jeweiligen Endpunkt berechnen, sowie die richtige Farbe dazu bestimmen.
Noch besser wäre natürlich der Polygonzug (Kreisausschnitt), oder gleich eine Füllroutine, die die Ellipse füllt und bei der Bestimmung der jeweiligen Pixelfarbe auch Interpolationen berücksichtigt, statt übereinander zu zeichnen.
Ja. Andersherum iterieren ist wohl tatsächlich die beste Lösung. Ein Polygonzug oder eine Füllroutine beißen sich leider mit dem zweiten Schritt meines Projektes, bei dem ich die Linien anders sortiere (nicht farblich).
Der Effekt ähnelt einem Problem, dass ich mal beim "händischen" Drehen von Bildern hatte, ohne AffineTransform zu nutzen.
Ich habe dabei fälschlicherweise die Koordinaten eines Pixels des Quellbildes, um das Zentrum gedreht, und den Pixel an den Zielkoordinaten auf die Farbe des ursprünglichen Pixels gesetzt. Klingt naheliegend, oder? Funktioniert aber nicht und ergibt viele leere Stellen, die entfernt an die leeren Bereiche deiner Ellipse erinnern.
Die Lösung war, den Pixel aus dem Zielbild entgegengesetzt (!) zu drehen, und falls diese Koordinaten innerhalb des Quellbildes lagen, die entsprechende Pixelfarbe von dort zu übernehmen.
Statt also das Quellbild im Uhrzeigersinn zu drehen, wird das Zielbild entgegen gesetzt dem Urzeigersinn gedreht.
Die Lösung war also - wie so oft in der Mathematik - das Ganze von hinten anzugehen!
Zu deinem Problem mit der Ellipse: Das kannst du lösen, indem du keine Linien mehr zeichnest, sondern Dreiecke, bei denen zwei Punkte benachbarte Linienenden am Rand sind, und der dritte Punkte im Mittelpunkt der Ellipse liegt.
Wie du den tollen Effekt mit der Rot- / Blau-Separation hinbekommen hast, weiß ich aber nicht. Sieht aber interessant aus! :)
Danke für die Antwort!
Zu deinem Problem mit der Ellipse: Das kannst du lösen, indem du keine Linien mehr zeichnest, sondern Dreiecke, bei denen zwei Punkte benachbarte Linienenden am Rand sind, und der dritte Punkte im Mittelpunkt der Ellipse liegt.
Wäre eine mögliche Lösung, aber keine für mein Projekt - ich brauche definitiv Linien.
Wie du den tollen Effekt mit der Rot- / Blau-Separation hinbekommen hast, weiß ich aber nicht. Sieht aber interessant aus! :)
Das habe ich mittlerweile herausgefunden - ich Depp habe mit Degree statt Radian gerechnet.
Hallo Willibergi,
ich möchte mich jetzt nicht in den Code vertiefen, aber folgendes:
wahrscheinlich liegt die unschöne Darstellung daran, dass du vom Zentrum aus die Linien Richtung Ellipsenrand zeichnest und von einer Linie zur nächsten den Winkel vergrößerst.
Je weiter zwei benachbarte Linien vom Zentrum entfernt sind, umso weiter sind zwei benachbarte Punkte P(linie_1) und P(linie_2) entfernt. Dadurch entstehen "Löcher", also Pixel, auf die nicht gezeichnet wird.
Ich würde es umgekehrt versuchen: die Linien von der Ellipse ins Zentrum zeichnen. Dabei rechnest du nicht mit Winkeln, um von einer Linie zur nächsten zu gelangen, sondern du verbindest ein Pixel, das auf der Ellipse liegt, mit dem Zentrum durch eine Linie. Dann nimmst du das nächste Pixel der Ellipse und verbindest es mit dem Zentrum usw.
Dabei werden zwar einige Pixel mehrfach überzeichnet, aber es wird keine Lücken geben. Verstehst du, wie ich das meine?
Dadurch wärst du auch unabhängig von der Auflösung.
Gruß
Das würde auch funktionieren. Müsste man mal probieren bei welcher Lösung das Ergebnis am "schönsten" ist.
Genau, wobei ich nicht weiß, welchen Farbvorstellung Willibergi hat.
Soll die Farbe auf einer Linie konstant sein, oder soll sie ein gewisses Farbspektrum durchlaufen - in Abhängigkeit von der Länge der Linie, oder...
Jede Linie hat eine Farbe und die Linien nebeneinander ergeben dann die "Farbkreisellipse" mit den weich wirkenden Übergängen. Genau so wie das Dreieck oben auch, das besteht auch nur aus Linien. Nur möchte ich es eben elliptisch.
Danke für Deine Antwort!
Oh ja, das ist kein schlechter Ansatz. Klingt nur trivialer, als er ist, einfach umgekehrt zeichnen würde ja nichts ändern. Mir erschließt sich nur gerade nicht ganz, wie ich alle Pixel der Ellipse systematisch durchgehen kann - der mathematische Ansatz, den ich verwende, dürfte ja nicht großartig anders sein... entweder stehe ich gerade selbst gewaltig auf dem Schlauch oder ich müsste die Berechnung grundsätzlich nochmal umdenken... aber der Ansatz ist top - danke!
Ja, das stimmt schon mit dem "Von außen nach innen zeichnen". Das würde erstmal nichts ändern. Man sieht auf deinem Bild ja schon, dass du nicht alle Punkte des Randes "erwischt". Das muss auf jeden Fall gegeben sein, auch wenn Du die Skalierungsmethode verwendet.
Gurß
Ein Problem dabei ist, dass die Anzahl der Linien bereits konstant ist (3*255). Du benötigst für größere Ellipsen mehr Linien. Das siehst Du auch daran, dass eine Ellipse (30,15) gar nicht mehr so schlimm aussieht.
Gruß
Die einzige Möglichkeit, die ich momentan sehe, ist, mit der Definition meiner Ellipse als Kurve zu rechnen und dann vom Pixel (x | k(x)) auf den Punkt (x+1 | k(x+1)) zu schließen. Dann müsste ich auf jeden Fall jeden Pixel erwischen.
Tatsache. Aber mehr Farben bekomme ich nicht, weil ich ja schon den gesamten RGB-Farbraum ausgeschöpft habe. Ich habe gerade mal versucht, den Stroke der Linien zu ändern, um zumindest einen Ansatz der Zeichnung zu sehen, aber irgendwie funktioniert auch das nicht: https://i.ibb.co/1ZBfr47/image.png
Kann es sein, dass das nicht das einzige Problem ist? Ich habe ein bisschen das Gefühl, als würden gleiche Farben nicht nebeneinander, sondern in einem bestimmten Winkelabstand in der Ellipse gezeichnet werden - zumindest sieht es auf dem Bild so aus.
Klingt nur trivialer, als er ist, einfach umgekehrt zeichnen würde ja nichts ändern.
Jetzt verstehe ich.
Stimmt, das ändert nichts, wenn du weiterhin mit Winkeln rechnest.
Wenn du aber mit Pixelkoordinaten rechnest, dann verbindest du das Zentrum mit jedem Pixel der Ellipse. In der Tat ist dann egal, ob von innen nach außen oder umgekehrt. Halt "nur" den Winkel fallenlassen und nur mit den Koordinaten der Pixel, die auf der Ellipse liegen, rechnen.
PS: Wenn ich die Leistung meines Computers künstlich drastisch verringere, sehe ich wie die Linien gezeichnet werden - das kann doch nicht richtig sein?
Ja, das stimmt, das ist wohl die technisch bessere Lösung. Ich werde mich mal dranmachen, die Berechnung so umzuschreiben.
Ic bin zwar kein Java-Programmierer, es gibt jedoch in jeder grafikfähigen Programmiersprache eine PieSlice() oder PieChart funktion etc. .
Verwendest du statt Linien "Kuchenstücke" klappt es mit dem Nachbarn... auch ohne weiße Lücken.
https://stackoverflow.com/questions/15167276/drawing-slices-of-a-circle-in-java
https://docs.oracle.com/javase/tutorial/2d/overview/index.html
http://www.java2s.com/Tutorial/Java/0261__2D-Graphics/DrawingaPieChart.htm
Kreisteile zu zeichnen, ist zwar grundsätzlich keine schlechte Idee, kommt aber für mein Projekt leider nicht infrage, weil ich definitiv Linien benötige. Aber trotzdem danke für die Antwort!
Danke für Deine Antwort!
Aber ist das nicht dasselbe, wie als würde ich einfach größer zeichnen?