2 Antworten
Ich seh das wie folgt.
Berechnung
a = Wurzel( (e/2)² + (f/2)² )
a = Wurzel( (9/2)^2 + (12/2)^2 )
a = 7,5 cm
---
b = a
b = 7,5 cm
---
Grundfläche
G = e * f / 2
G = 9 * 12 / 2
G = 54 cm²
---
Oberfläche
O = (G * 2) + ((a * 2) + (b * 2) * h)
O = (54 * 2) + (((7,5 * 2) + (7,5 * 2)) * 14)
O = 528 cm²


Bei der Aufgabe stimmt was nicht . Aber es hat sich geklärt dank Mercurus . Schaue jetzt unten
Mit den Maßen ist es kein Prisma , sondern ein Pyramidenstumpf (auf dem Kopf stehend)
.
man muss die Maße der Boden - und Deckfläche bestimmen
.
sie ist rechteckig mit Breite B und Tiefe T
.
Oben gilt mit Pythagoras
12² = B² + T²
Unten gilt
9² = B² + T²
.
Umstellen zu T²= oder B²= und gleichsetzen
12² - T² = 9² - T²
was zu 144 = 81 führt
Keine wahre Aussage
Kein Wunder : In Rechtecken sind die Diagonalen ja auch gleich lang
.
Es ist eine Raute : die Diagonalen halbieren sich und stehen senkrecht aufeinander

darum ist die Seite s durch
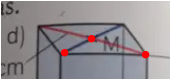
Vielen Dank für die die verbesserte Antwort :)))

Du gehst von der falschen Annahme aus, die Grundfläche sei ein Rechteck - bemerkst aber gleichzeitig, dass das nicht sein kann.
Natürlich gibt es Vierecke, deren Diagonalen verschiedene Länge haben und senkrecht aufeinander stehen.