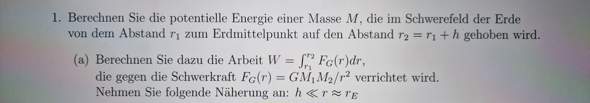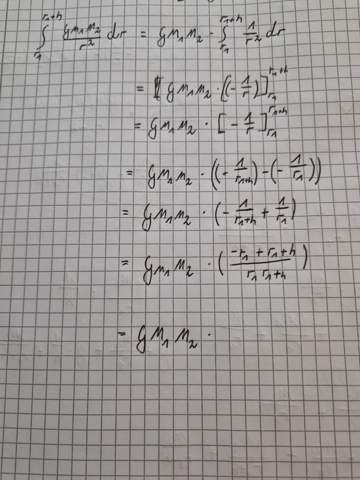Hallo, nette Leser!
Es geht um folgendes: im folgenden Link - weiter unten - unter der Überschrift "Potentielle Energie Epot" - unter der Teilüberschrift "Potentielle Energie in inhomogenen Feldern"
http://www.abi-physik.de/buch/das-elektrische-feld/elektrische-felder-2/
Dort geht es um die potentielle Energie in einem radialsymmetrischen Feld. Es steht geschrieben: "Bei einem inhomogenen Radialfeld um eine Punktladung herum, wird meist festgelegt, dass die potentielle Energie in unendlicher Entfernung von der Punktladung = 0 ist."
Man geht anscheinend davon aus, dass die Punktladungen entweder beide positiv oder beide negativ geladen sind.
Was ist aber wenn die erste Punktladung A, um dessen Feld es geht, positiv geladen ist, die zweite Punktladung B, dessen potentielle Energie im Feld der ersten Punktladung berechnet werden soll, aber negativ geladen ist. Wäre es nicht sinnvoller festzulegen, dass die potentielle Energie direkt an der ersten Punktladung A 0 ist statt in unendlicher Entfernung davon?
Wenn ja - könnte man die potentielle Energie der Punktladung B im Feld der Punktladung A immer noch mit derselben Formel berechnen, die dort angegeben ist oder müsste man dort was umstellen? Wenn nein - wieso nicht? Kann mir jemand den Sachverhalt dort bitte ein bisschen verständlicher erklären?
Vorabinfo: Ich bin mir über die Herleitung bzw. wieso die Formel des Coloumbschen Kraftgesetzes funktioniert bewusst. Die Herleitung der Formel für die Energieänderung in einem radialsymmetrischen Feld ist mir nur semi bewusst. Ich weiß, dass es was mit dem integrieren der Formel des Coloumbschen Kraftgesetzes zu tun hat. Darum soll es aber hier primär auch nicht gehen. Mich interessiert primär der Sachverhalt mit der potentiellen Energie.
Schonmal großen Dank in Vorraus an alle Antworten und Mühen!! :)
Mit freundlichsten Grüßen JK