Graph anhand funktion skizzieren?
Ganzrationale funktion: f (x)= 0,5x^3 - 6x +3 Aufgabe: Skizziere einen Graphen Was ich bereits weiß : der graph kommt von links aus dem - Bereich (-unendlich) wegen der ^3; die Steigung hat was mit der -6x zu tun ; der graph schneidet die y-Achse am Punkt 3 Meine fragen : was sagt die 0,5 vor dem x^3 aus? ; wie soll ich den graphen nun skizzieren woher weiß ich wo er wieder hoch / runter geht und geht er am Ende wieder ins unendlich positive oder negative? ? Hier ist die Lösung (siehe bild) ich kann das aber nicht nachvollziehen warum der jetzt so aussieht
4 Antworten
Du kannst mit Hilfe der Ableitung den Graphen noch genauer skizieren.
Dazu bildest du dann erst einmal die Ableitung f' :
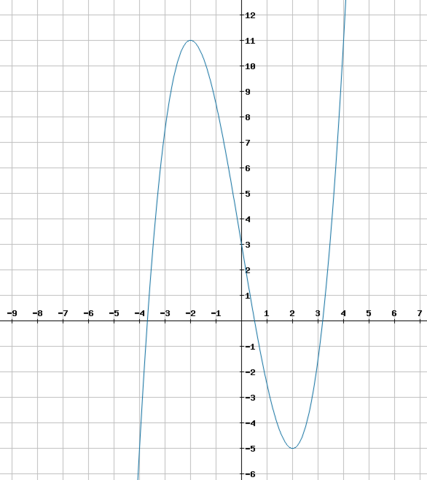
f(x) = 0,5x³ - 6x + 3 ---> Bild 1
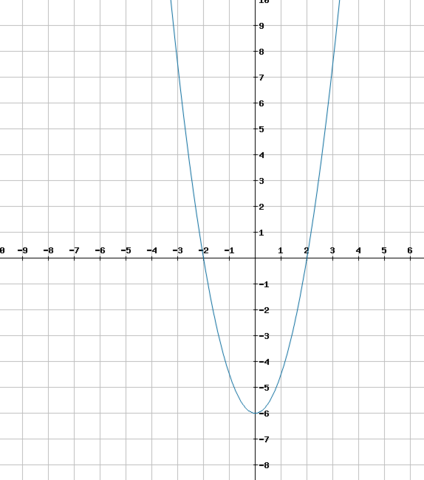
f'(x) = 1,5x² - 6 ---> Bild 2
Nun kannst du die Nullstellen dieser Funktion ausrechnen.
Notwendige Bedingung:
f'(x) = 0
1,5x² - 6 = 0 |+6
1,5x² = 6 |:1,5
x² = 4 |√
x1 = 2
x2 = -2
►►Die Nullstellen der Ableitungsfunktion f'(x) sind die Extremstellen der Ausgangsfunktion f(x).
Das heißt, der Graph der Ausgangsfunktion f(x) hat bei x1 = 2 und x2 = -2 seine Extrempunkte.
Dort wendet der Graph also, sofern kein Sattelpunkt vorliegt. Da auch keine doppelte Nullstelle vorhanden ist, berührt der Graph auch nicht nur die x-Achse, sondern schneidet sie wirklich.
Nun kannst du dir ein Koordinatensystem machen und dort die bekannten Informationen eintragen.
Du kannst sogar noch weiter gehen und die berechneten Nullstellen der Ableitungsfunktion in die Ausgangsfunktion einsetzten, um die genauen Punkte zu bestimmen:
f(2) = 0,5 * 2³ - 6 * 2 + 3
f(2) = 4 - 12 + 3
f(2) = -5
________________________
f(-2) = 0,5 * (-2)³ - 6 * (-2) + 3
f(-2) = -4 + 12 + 3
f(-2) = 11
P1 ( -2 | 11 ) ; P2 ( 2 | -5 )
Dort sind also die Extrempunkte. Welcher genau, kannst du so noch nicht sagen. Dafür müsstest du die Nullstellen in die 2. Ableitung einsetzen oder das Vorzeichenwechsel-Kriterium betrachten, was man sich hier aber sparen kann.
In dein gezeichnetes Koordinatensystem zeichnest du nun einfach zusätzlich zu den anderen Informationen diese beiden Punkte ein. Da der Graph aus den negativ Unendlichen (-∞) komm und am "Ende" ins positiv Unendliche (+∞) verläuft und du nur 2 Extrempunkte hast und es keine doppelte Nullstelle gibt weißt du, dass der Graph an den beiden Extrempunkten wenden muss. Es sind also entweder Hoch- oder Tiefpunkte. Sattel-/Terassenpunkte sind hier ausgeschlossen.
Deswegen zeichnest du einfach von unten aus dem negativ unendlichen raus bis zum ersten Extrempunkt bei P1 ( -2 | 11 ). Dort wendet sich der Graph. Ab dem Extrempunkt fällt der Graph also streng monoton. Das ganze bis er den zweiten Extrempunkt P2 ( 2 | -5 ) erreicht hat. Von dort an ist der Graph bis ins positiv unendliche wieder streng monoton steigend.
_________________________________________________________
Ich bin mir nicht ganz sicher, ob dir das ganze überhaupt was sagt. Ob ihr schon die Ableitung kennen gelernt habt...
Falls dir das Hilft hast du hier noch einmal ein Video von TheSimpleMaths zu den Grundlagen der Ableitung:
https://youtube.com/watch?v=4L9s2GHZCq0
Hier findest du auch noch einen kleinen Artikel zu der Bedeutung der 1. Ableitung:
http://www.mathebibel.de/erste-ableitung
_________________________________________________________
Falls du also irgendwas nicht verstehst und du Fragen hast, beantworte ich sie dir gerne! ;)
Liebe Grüße
TechnikSpezi
Meine fragen : was sagt die 0,5 vor dem x^3 aus?
Der Vorfaktor vor dem x³, also hier die 0,5, sind das, was man damals bei den quadratischen Funktionen noch den Vorfaktor a, also den Stauch- und Streckfaktor genannt hat.
Damit stauchst und streckst du den Graphen entland der y-Achse.
Bei ganzrationalen Funktionen wird dieser Faktor aber ziemlich unwichtig, da du du hier nicht mit Wertetabellen arbeitest. Deswegen ist der Faktor eher zu vernachlässigen. das einzig wichtige daran ist, ob der Faktor positiv oder negativ ist.
Nunja. Also zunächst einmal ist der Graph punktsymmetrisch zu (0,3). Wie du richtig festgestellt hast, geht er für x gegen -unendlich gegen -unendlich und analog für x gegen unendlich auch gegen unendlich.
Die 0.5 verlangsamen (bildlich gesprochen) das Wachstum. Dadurch wird der Graph in y-Richtung gestaucht.
Zum skizzieren empfiehlt es sich, die Nullstellen noch auszurechnen, sowie die Extremalstellen (Nullstellen der 1. Ableitung, etc.). Danach solltest du in der Lage sein die ermittelten Punkte zu einer Skizze des Graphen zu verbinden.
Mit einem Taschenrechner die Gleichung 0 = 0.5x^3 - 6x + 3 lösen. Per Hand sollte das hier nicht möglich sein.
Berechne die Extremwerte die Nullstellen und dei Steigungen in den Nullstellen und die Steigung beim Schnitttpunkt der y-Achse.
Wenn du all dies einzeichnest, hast du schon ein ganz gutes Bild des Graphen!
Wie rechne ich die nullstellen bei dieser art von funktion aus?
Das ginge bei dieser Form z.B mit der Cardanischen Formel - aber das dürfte hier zu weit führen.
(Hier zum Nachlesen:
https://de.wikipedia.org/wiki/Cardanische_Formeln
)
Es wäre für dieses Beispiel wohl übers Ziel hinausgeschossen.
Statt der Nullstellen nimmst du einfach ein oder zwei Werte links des am weitest links liegenden Extremwertes, ein oder zwei Werte rechts des am weitest rechts liegenden Extremwertes und ein oder 2 Werte zwischen den Extremwerten. - jeweils mit den Steigungen.
Im Prinzip überlegst du dir die prinzipielle Form (diese kann man anhand des Grades "erraten" oder über die Nullstellen der Ableitung herausfinden) und setzt dann ein paar Punkte ein.
Die höchste Potenz gibt vor, was der Graph in den Bereichen Richtung unendlich macht.
x³ also geht es bei - ist negative und bei + ins positive
die 0,5 davor geben dir an, das er flacher als normal ist, die Werte sind halb so hoch.
+3 bedeutet, der Graph ist um 3 nach oben verschoben.
-6x ist eine lineare Funktion, diese kannst du dir als Hilfe auch hinmalen, sie wird entsprechend zu den anderen Werten addiert und sorgt im Bereich nahe der y-Achse für starke Verschiebungen, da dort die x³ Funktion ja sehr kleine Werte hat.
Wie soll ich den graph dann skizzieren? Mir der 0.5 undso?
Du wirst die Nullstelle(n) ausrechnen und den Schnittpunkt mit der y-Achse. Dann wirst du in den Bereichen, wo du dir nicht sicher bist einfach ein paar Punkte ausrechnen und diese einzeichnen. Dann Verbindest du die Punkte mit dem Wissen, welches du durch die obigen Aussagen gewonnen hast.
Wie rechne ich die nullstellen bei dieser Funktion aus?
Wie rechne ich die 0 stellen bei dieser art von funktion aus?