Geometrie (Vektoren)?

Hallo Leute kann jemand mir sagen ,warum bei der Frage a) der Winkel ABC muss 146,44 und nicht 33,55 sein

Answer 1

[mihisu]

$A\left(\,2\,\middle|\,-3\,\middle|\,7\,\right),\quad B\left(\,1\,\middle|\,4\,\middle|\,9\,\right),\quad C\left(\,-3\,\middle|\,-4\,\middle|\,5\,\right)$

$\overrightarrow{BA}=\begin{pmatrix}2-1\\-3-4\\7-9\end{pmatrix}=\begin{pmatrix}1\\-7\\-2\end{pmatrix}$

$\overrightarrow{BC}=\begin{pmatrix}-3-1\\-4-4\\5-9\end{pmatrix}=\begin{pmatrix}-4\\-8\\-4\end{pmatrix}$

$\overrightarrow{BA}\bullet \overrightarrow{BC}=\begin{pmatrix}1\\-7\\-2\end{pmatrix}\bullet\begin{pmatrix}-4\\-8\\-4\end{pmatrix}$

$\quad = 1\cdot (-4)+(-7)\cdot (-8)+(-2)\cdot (-4)$

$\quad =-4+56+8=60$

$\left\lvert \overrightarrow{BA}\right\rvert=\sqrt{1^2+\left(-7\right)^2+\left(-2\right)^2}=\sqrt{1+49+4}=\sqrt{54}$

$\left\lvert \overrightarrow{BC}\right\rvert=\sqrt{\left(-4\right)^2+\left(-8\right)^2+\left(-4\right)^2}=\sqrt{16+64+16}=\sqrt{96}$

$\cos(\sphericalangle ABC)=\frac{\overrightarrow{BA}\bullet\overrightarrow{BC}}{\lvert \overrightarrow{BA}\rvert\cdot \lvert \overrightarrow{BC}\rvert}=\frac{60}{\sqrt{54}\cdot \sqrt{96}}=\frac{60}{\sqrt{54\cdot 96}}=\frac{60}{\sqrt{5184}}=\frac{60}{72}=\frac{5}{6}$

$\sphericalangle ABC=\cos^{-1}\left(\frac{5}{6}\right)\approx 33\text{,}56\degree$

============

Vermutlich hast du bei deiner Berechnung den Vektor AB statt den Vektor BA verwendet. [Damit hast du den entsprechenden Außenwinkel des Dreiecks berechnet, statt den gesuchten Innenwinkel.]

Du brauchst hier aber, da es um den Winkel bei B geht, die entsprechenden Vektoren mit B als Fußpunkt, also die Vektoren BA und BC.

Comments

[Willy1729]

-Den Vektor (-4/-8/-4) kannst Du getrost zu (1/2/1) kürzen; das macht das Rechnen etwas einfacher.

[mihisu]

@Willy1729

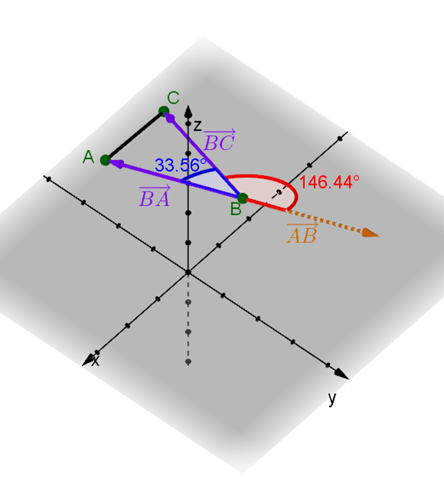
Nein, das kann man hier nicht so einfach. Denn (1, 2, 1) zeigt in die entgegengesetzte Richtung wie (-4, -8, -4).

Für den cos-Wert würde man dann -5/6 statt 5/6 erhalten.

Damit wäre man wieder genau beim Problem des Fragestellers, da man dann den Winkel mit etwa 146,44° statt den gesuchten Winkel mit etwa 33,56° erhalten würde.

[Willy1729]

@mihisu

Ich nehme den Betrag des Zählers, also 15 statt -15. So bekomme ich auch 33,56° heraus.

[mihisu]

@Willy1729

Und dann begründe mal dem Fragesteller, warum du da einfach Betrag nimmst und es dann wieder richtig wird.

============

Und was wäre nun in einem anderen Beispiel? Wenn beispielsweise A(1|-7|-2), B(0|0|0), C(4|8|4) wäre. Würdest du dann auch den Vektor (1, 2, 1) statt den Vektor BC mit (4, 8, 4) verwenden und dann auch den Betrag des Zählers verwenden, wenn du den Winkel ABC berechnen sollst? Dann würdest du aber in diesem anderen Beispiel den falschen Winkel von etwa 33,56° erhalten, da in diesem anderen Beispiel tatsächlich etwa 146,44° richtig wäre.

Und wenn du da nicht den Betrag verwenden würdest... Warum verwendest du in einem Fall den Betrag und in dem anderen Fall nicht?

Das sind alles Dinge, die den Fragesteller verwirren würden. Und genau wegen sowas kommt man dann auf 146,44° statt 33,56° oder umgekehrt, worum es ja gerade in der Frage des Fragestellers geht, dass er evtl. so einen Fehler gemacht hat.

Daher habe ich das nicht in meine Antwort aufgenommen, sondern bin einfach relativ stur nach Formel vorgegangen, ohne da irgendwelche andere Vektoren zu nehmen.

[Willy1729]

@mihisu

Ich merke gerade, daß ich die Formel falsch im Kopf hatte - vom Betrag des Skalarprodukts steht da ja gar nichts.

Answer 2

[MichaelH77]

ich komme auch auf 33,55°

das ist der Winkel zwischen den Vektoren BA und BC

$\beta=\cos^{-1}\left(\frac{1\cdot\left(-4\right)+\left(-7\right)\cdot\left(-8\right)+\left(-2\right)\cdot\left(-4\right)}{\sqrt{1+49+4}\cdot\sqrt{16+64+16}}\right)=\cos^{-1}\left(\frac{5}{6}\right)=33.6°$

Answer 3

[Willy1729]

Hallo,

auf den größeren Winkel kommst Du, wenn Du den Zähler negativ läßt und nicht den Betrag nimmst, wie es in der Formel eigentlich vorgesehen ist.

Nachtrag: In den Zähler gehört nur das Skalarprodukt, nicht dessen Betrag. Ich hatte zwei Formeln durcheinandergeworfen.

Herzliche Grüße,

Willy