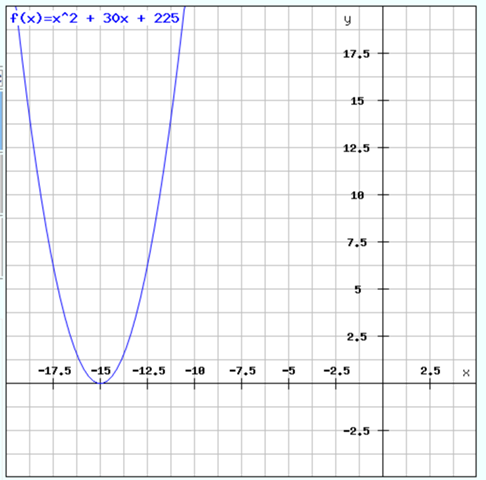
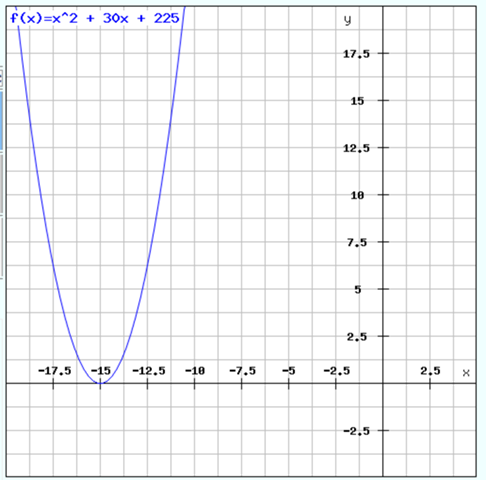
Wie kann man die Funktionsvorschrift angeben, deren Graph eine verschobene Normalparabel mit dem Scheitelpunkt S ist?
Hey Leute,
ich habe Probleme bei meiner Hausaufgabe oben auf der Überschrift steht die Aufgabe und jetzt ist der Scheitelpunkt S(-15|0) gegeben kann mir jemand zeigen wie man da die Vorschrift der Funktion angibt.
3 Antworten
Hallo,
allgemeine Scheitelpunktform einer Parabel:
y=a*(x-d)²+e, wobei der Scheitelpunkt die Koordinaten (d|e) besitzt und a der Streckungsfaktor der Parabel ist. Bei einer Normalparabel ist a=1.
Herzliche Grüße,
Willy
y=(x+15)²
durch Ausrechnen der binomischen Formel kannst du die Funktion auch in die allgemeine Parabelgleichung bringen
Ich fasse mal das wichtigste zusammen, was man unbedingt zu Parabeln wissen muss.
a) Definitionen
Quadratische Funktion: eine quadratische Funktion liegt dann vor, wenn in der Funktionsgleichung ein x^2 als höchste Potenz vorkommt.
Parabel: Eine Parabel ist der Graph einer quadratischen Funktion
Normalparabel: eine Normalparabel liegt dann vor, wenn vor dem x^2 kein Faktor steht, wenn das x^2 sozusagen alleine dasteht.
b) Darstellungsformen
Die Funktionsgleichung zu Parabeln lässt sich grundsätzlich in drei verschiedenen Darstellungsformen schreiben, die aber alle zum selben Ergebnis, also zum selben Graphen führen.
Was vor dem Gleichheitszeichen steht, ist nicht eindeutig festgelegt. Üblich sind y = ..... oder f(x) = ….. Aber auch andere Bezeichnungen vor dem Gleichheitszeichen sind möglich.
1) Die Normalform lautet:
f(x) = ax^2 + bx + c
In der Normalform sind alle Klammern ausmultipliziert und die x sind nach ihrer Hochzahl geordnet.
2) Die Scheitelpunktform beruht auf den Koordinaten des Scheitelpunktes. Wenn der Scheitelpunkt die Koordinaten S(d/e) hat, lautet die Scheitelpunktform:
f(x) = a(x - d)^2 + e
d ist die x-Koordinate und e ist die y-Koordinaten des Scheitelpunktes.
3) Die Nullstellenform beruht auf den x-Werten der Nullstellen der Funktion. Das sind die Stellen, bei denen der Graph die x-Achse schneidet. Die Nullstellenform hat eine Besonderheit. Während man jede Parabel in der Normalform oder Scheitelpunktform darstellen kann, ist das bei der Nullstellenform nur dann möglich, wenn die Parabel so liegt, dass sie die x-Achse auch tatsächlich schneidet. Das ist aber nicht immer der Fall.
Die Nullstellenform lautet:
f(x) = f(x) = a(x - xo1) * (x - xo2)
xo1 und xo2 sind die beiden Nullstellen der Funktion, also die x-Werte, bei denen die Parabel die x-Achse schneidet.
c) Der Streckungsfaktor a
Eine Parabel kann flach und breit (gestaucht) oder schmal und steil (gestreckt) sein. Das hängt vom sogenannten Streckungsfaktor a ab. Egal welche der drei Darstellungsformen man wählt, a hat immer denselbe Wert. Der Streckungsfaktor a bestimmt das Aussehen der Parabel:
a = 1: Das ist die nach oben geöffnete Normalparabel. Üblicherweise lässt man a = 1 in den Gleichungen ganz weg.
a ist positiv: die Parabel ist nach oben geöffnet
a ist negativ: die Parabel ist nach unten geöffnet
Betrag von a ist kleiner als 1: die Parabel ist flacher als die Normalparabel
Betrag von a ist größer als 1: die Parabel ist schmaler als die Normalparabel
d) Umrechnungen von einer Form in die andere
Alle drei Darstellungsformen der quadratischen Funktion/Parabel lassen sich ineinander umrechnen.
1) Von der Normalform in die Scheitelpunktform: da wendet man die quadratische Ergänzung an
2) Von der Normalform in die Nullstellenform:
Man setzt f(x) = 0 und löst diese quadratische Gleichung entweder mit der pq-Formel oder der Mitternachtsformel. Die Nullstellen setzt man dann, wenn es welche gibt, in die Nullstellenform ein.
3) Von der Scheitelpunktform oder der Nullstelllenform in die Normalform: dazu mulitpliziert man die Klammern aus und sortiert die x nach ihrer Hochzahl.
----------------------------------------------------------------------------------------------------------------------------------
So, mit dem, was ich bisher geschrieben habe, lässt sich auch deine Aufgabe leicht lösen.
Information: es handelt sich um eine Normalparabel.
logischer Schluss: a = 1, kann als entfallen
Information: gegeben ist der Scheitelpunkt
Ansatz: da wählen wir die Scheitelpunktform als Ansatz:
S(-15/0), damitlautet die Schweitelpunktform:
f(x) = (x -(-15))^2 + 0 = (x + 15)^2
Die müssen wir nun in die Normalform umrechnen, indem wir die Klammer ausmultiplizieren:
f(x) = x^2 + 2 * 15 * x + 15^2 = x^2 + 30x + 225
Ergebnis:
Die Scheitelpunktform lautet f(x) = (x + 15)^2
Die Normalform lautet: f(x) = x^2 + 30x + 225
Und so sieht der Graph dazu aus: