Für welchen Wert hat der Graph eine Nullstelle?

Guten Abend, ich sitze jetzt schon seit einer Weile an der beigefügten Aufgabe und komme einfach nicht weiter. Ich wäre euch sehr dankbar, wenn mir jemand eventuell erläutern könnte wie man diese Aufgabe löst.
lg
2 Antworten
a)
Damit lautet die Funktion:
f(x) = 2x^2 + 4x + d
Die soll genau eine Nullstelle haben:
2x^2 + 4x + d = 0
x^2 + 2x + d/2 = 0
Nun die pq-Formel, die genau dann eine Lösung hat, wenn die Wurzel = 0 ist.
p = 2; q = d/2
Der Ausdruck unter der Wurzel lautet:
(p/2)^2 - q
und das soll = 0 sein:
(2/2)^2 - d/2= 0
1 - d/2 = 0
d = 2
Damit lautet die Funktion mit genau einer Nullstelle:
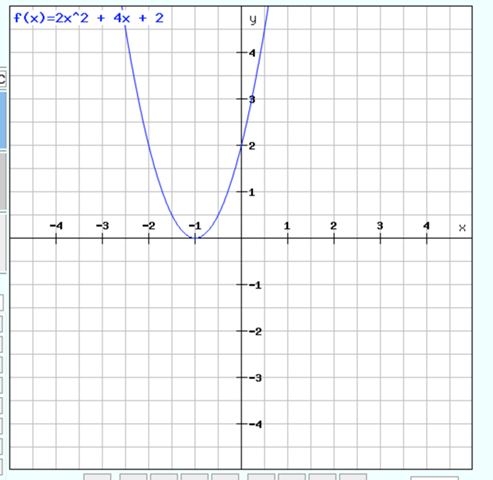
f(x) = 2x^2 + 4x + 2
Probe mit einem Funktionsplotter:
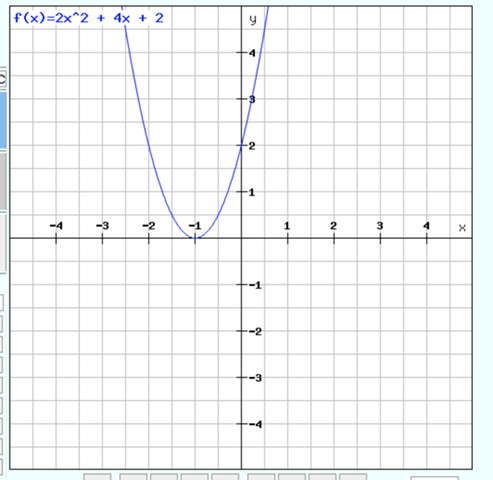
b) Für das Verhalten eines Graphen für x gegen unendlich ist immer die höchste Potenz verantwortlich. Bei der gegebenen Funktion wäre für a ungleich 0 das ax^3 die höchste Potenz.
Damit bestimmt der Parameter a das Verhalten der Funktion für x gegen unendlich aber nur dann, wenn a unglleich 0 ist. Wenn a gleich 0 ist, ist bx^2 die höchste Potenz und dann bestimmt b das Verhalten der Funktion.
Vielen Dank für die ausführliche Antwort. Ich habe es nun endlich verstanden.
Hehe.
Nutze die PQ-Formel und schau Dir die Wurzel genauer an. 🙂
PQ- Formel benutzen --> 4² - 4 * 2 * d = 0
Das nach d auflösen. --> 16 - 8d = 0
<=> d = 2.
Für d = 2 gibt's genau eine reelle Lösung.