Für reelle Werte a sei die Funktionsschar fa(x)= (x-a)•e^x gegeben. Weisen Sie nach, dass alle Graphen der Funktionsschar ein lokales Minimum in x=a-1 haben?

Guten Tag, ich schaue mir gerade alte Aufgaben von mir an, um für eine Klausur zu üben, aber verstehe ich gar nicht, wie ich bzw. wir vorgegangen sind. Ich habe die Bearbeitung in den Anhang getan, weil das übersichtlicher ist. Einfache Ansätze verstehe ich noch, aber ich verstehe das Ableiten und Umformen nicht. Ich wäre sehr dankbar, wenn mir das jemand erklären könnte.
Liebe Grüße Anna

Answer 1

[verreisterNutzer]

Der Reihe nach:

Da wurde ganz einfach e^x ausgeklammert (manchmal hilft vom Ergebnis her rückwärts rechnen dem Verständnis enorm)

$e^x+\left(x-a\right)\cdot e^x=1\cdot e^x+\left(x-a\right)\cdot e^x=e^x\cdot\left(1+\left(x-a\right)\right)$

Und die innere Klammer kann man dann auch weglassen

Satz vom Nullprodukt (Du Exponentialfunktion kann nicht 0 werden, also bleibt nur die Möglichkeit, dass der Faktor davor 0 wird):

$\left(x+1-a\right)\cdot e^x=0\ \Leftrightarrow\left(x+1-a\right)\ =\ 0\ \Leftrightarrow x\ =\ a-1$

Da verstehe ich die Frage ehrlich gesagt nicht wirklich: Wenn man auf ein Minimum prüfen will, prüft man in der Regel, ob f''(x) >0 an der Nullstelle der ersten Ableitung ist. Also berechnet man die 2. Ableitung (ist das Dein Problem?) und setzt dann die Nullstelle der 1. Ableitung ein, also hier f''(x = a -1) =f''(a - 1) (liegt Dein Problem hier?) und wie schon oben geschrieben, kann die Exponentialfunktion nicht null werden.

Comments

[Martinamey]

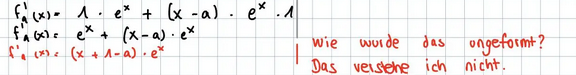
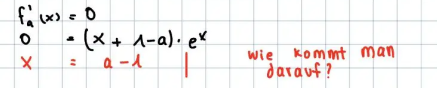
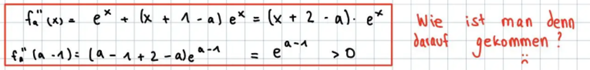
Vielen lieben Dank für deine mühevolle Arbeit! Das schätze ich sehr wert.