Extremwertaufgabe
Habe eine Aufgabe zur Extremwertrechnung.
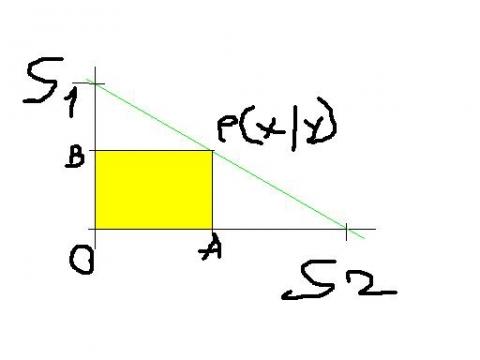
Gegeben ist eine Gerade mit g=-6/5x + 4 Innerhalb dieser Geraden soll die größtmöglichste Fläche des Rechtecks berechnet werden. Also der Punkt P.
Hoffe mir kann jemand bei dieser Aufgabe helfen.
2 Antworten
Also,
Formel zur Berechnung der Fläche vom Rechteck: ab. Definieren wir mal den Punkt A=(x,0) und B=(0,f(x)) d.h. dein Rechteck hat die Fläche F=xf(x) Was eine von x und deiner Geraden f(x) abhängige Funktion ist. Jetzt davon die Extremstelle ausrechnen und in deine Geradengleichung einsetzen. Und schon hast du x und y von P.
hallo P(1 2/3 ; 2) deine rechtecksfläche ist F=x mal y und für y setzt du die gerade g ein also F=x(-6/5 x + 4) und multiplizierst aus und F=-6/5 x² + 4x und jetzt wegen größte fläche F ' = -12/5 x +4 =0 und x= 1 2/3 und dann in gerade einsetzen, um y zu kriegen.y=2 gruß ej