Extremwert berechen Weidenfläche?
Hallo, es geht um folgende Aufgabe.
Schäfer Ansgar hat seine Schafherde an einen Fluss getrieben. Nachdem er gerade keinen Hund hat, will er der Schafherde mit insgesamt 120m Zaun eine rechteckige Fläche bauen. Wie sind die optimalen Abmessungen, sodass die Schafe also möglichst viel Platz haben? Welche Fläche hat in diesem Fall die Weide?
Muss Ich nun einfach die Fläche und die Nullstellen berechnen? Ich hab schon 3 Rechenwege versucht und es hat immer irgendwo gescheitert. Könnte mir da jemand beim rechenweg helfen?
"xs=30 ist der extremale Wert für die Funktion. Also = 30m, damit ist b = 60m. Der maximale Flächeninhalt ist also Amax = 1800m^2" Soll die Lösung sein
2 Antworten
Entlang des Flusses ist ein Zaun überflüssig. Es braucht nur quer zum Fluss die Seite und dann die Längsverbindung eingezäunt werden.
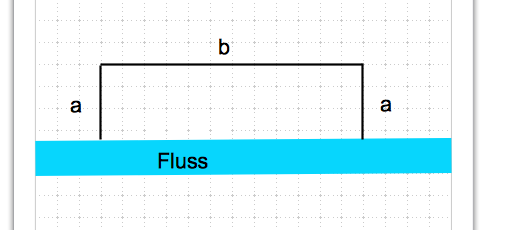
F = a * b
Hauptbedingung:
F = maximal
Nebenbedingung:
2a + b = 120
b = 120 - 2a
eingesetzt:
F = a (120 - 2a) = -2a^2 + 120a
F' = -4a + 120 = 0
4a = 120
a = 30
aus b = 120 - 2a folgt:
b = 120 - 2 * 30 = 60
F = a * b = 30 * 60 = 1800
Ergebnis:
Das Rechteck hat die Abmessung 30 m * 60 m und ist 1800 m^2 groß
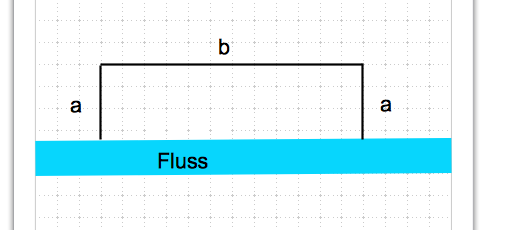
Bist du sicher, dass nicht irgendwo steht,
dass der Fluss die eine Seite des Rechtecks
bilden soll?
Dann hast du die Hauptbedingung
F = a*b = max
und die Nebenbedingung
2(a+b) = 120 --> a+b = 60
Die NB löst du z. B. nach b auf,
setzt es in die HB ein und bekommst
eine quadratische Gleichung. Die leitest du
ab, bei der Nullstelle der Ableitung ist das Optimum.
Tipp: Es wird ein Quadrat rauskommen..
Nein, die Aufgabe ist leider nur so gegeben, wie Ich sie da hin geschrieben habe :/