Exponentialfunktion aus 3 punken?
Hallo, man soll anhand von 3 Punkten die Funktion y = a * b^x + k finden. Über Eliminierung und substitution komme ich dann dazu, a = a zu setzen um damit b zu finden. Bei solchen Aufgaben kommt es bei mir sehr oft vor, dass ich am Ende ein Polynom dritten oder zweiten Grades mit drei oder zwei Lösungen bekomme. Hier war es auch so, dass ich über die ABC Formel 2 Lösungen bekommen habe, wovon eine (b=2) richtig ist. Woher weiß ich denn jetzt, welche der beiden Lösungen richtig ist für b ist?

3 Antworten
Hallo,
a=4, b=2, k=1, wenn's Dir hilft.
Bestimmungsgleichungen aus Gleichung 1 und 2: k=5-a und b=4/a+1 in Gleichung 3 einsetzen, dann nach a auflösen.
Herzliche Grüße,
Willy
Sackgassen sind dazu da, um Erfahrung zu bekommen - und Erfahrung ist für solche Aufgaben wichtig. Das wichtigste Handwerkszeug des Mathematikers ist der Papierkorb.
Haha okay, dann mache ich mal weiter. Danke.
Woher weiß ich denn jetzt, welche der beiden Lösungen richtig ist für b ist?
Wenn b=1 wäre, dann wäre es keine Expontentialfunktion, denn 1x ist immer eine Konstante (1x = 1 ∀ x ∈ ℝ)
Nur den ersten Satz lesen unter https://de.wikipedia.org/wiki/Exponentialfunktion. Dort stehen für die Basis (dort a genannt) die Bedingungen: a > 0 und a ≠ 1.
Skizze:

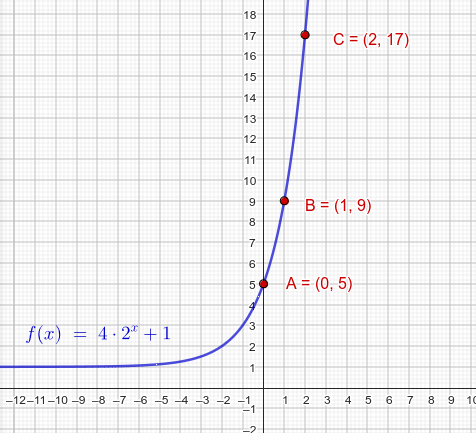
Achso, mein Fehler. Und wenn die beiden Lösungen valide wären? Also wenn sie b= 3 und b=4 wären? Woher weiß ich, welche richtig ist? Oder kommt es bei dieser Art Aufgabe immer vor, dass nur eine Lösung stimmen kann?
Kann es bei 3 (unabhängigen) Gleichungen und 3 Unbekannten mehr als 1 Lösung geben?
Nein, natürlich nicht. Villeicht habe ich das, wie auch hier, in meinen vorherigen Aufgaben übersehen, aber ich meine es gab Lösungen, die der standartform der gesuchten gleichung hätten entsprechen können, oder kann dies nicht der Fall sein? Heißt, muss ich jeweils immer eine Gegenprobe stellen oder wird die Antwort klar sein?
Einfach hinterher mit einer Probe ausprobieren ob alles stimmt oder deine gefundene Funktion in Geogebra zeichnen lassen und gucken ob sie so ist wie sie soll.
Es war doch so einfach.. Ich lande bei dieser Art Aufgabe oft in einer Sackgasse. Gibt es ein bestimmtes Prozedere bzw. Einen Vorgang, an dem man sich halten kann, damit genannte Sackgassen nicht vorkommen?