Exponential und Logarithmusfunktion erklären / erkennen?
Kann mir jemand in seinen eigenen Worten das alles erklären? Ich habe schon mehrere Videos mir angeschaut aber irgendwie nicht verstanden ...
Die Logarithmusfunktion spiegelt die Exponentialfunktion wieder, aber wie erkenne ich das nun in meinem Beispiel

Nummer b) meine ich damit und c) muss ich dazu auch machen. Ich brauche wirklich eine Erklärung warum es F3 ist
Bitte
2 Antworten
zu b):
Wenn man wüsste, dass die Log-Funktion nicht verschoben ist, könnte man sie alleine dadurch identifizieren, dass log(1), egal zu welcher Basis, immer 0 ist und damit durch den Punkt (1|0) gehen muss. Damit käme nur f₃ in Frage. (Und diese Funktion ist es auch.)
Wenn man aber nicht sicher ist, dass die Funktion nicht vielleicht verschoben ist, kann man sie mithilfe des Definitions- bzw. Wertebereichs eingrenzen.
Der Definitionsbereich der Logarithmusfunktion ist eingeschränkt, weil sie keine negativen Argumente haben kann. Gleichzeitig erstreckt sich der Wertebereich aber über ganz |R. Außerdem ist zu jedem x genau ein y (und nicht etwa mehrere y-Werte) zugeordnet.
Dadurch sind f₂ (keine eindeutige Zuordnung von y-Werten) und f₄ (eingeschränkter Wertebereich) aus dem Rennen.
Es sieht so aus, als ob die y-Achse eine Asymptote der Funktion f₃ ist, was zum eingeschränkten Defintionsbereich passen würde.
Außerdem sieht f₃ genau wie ln(x) aus und die Funktion f₁ eher so, wie e-Funktion verlaufen sollte.
Man könnte sich zwar auch eine Log-Funktion basteln, die aus links von ihrer Asymptote lebt, mit zunehmendem x eine größere Steigung hat und durch die Punkte (0|1) und (1|3) verläuft*, aber wenn man das mit der einfacheren Option f₃ vergleicht, kann man wohl davon ausgehen, dass f₃ die gesuchte Lösung sein soll.
zu c):
Diese Aufgabe ist deutlich einfacher.
Wenn a<1 ist, dann fällt die Exponentialfunktion (es sei denn, man hätte einen zusätzlichen Faktor c<0, was hier aber nicht zutreffend ist). Es kommen also nur f₁ und f₂ in Frage.
Da a⁰ für jedes a≠0 den Wert 1 annimmt, ist f(0)=c. c soll größer als 1 sein, was nur bei f₂ zutrifft.
Ergänzung:
Ich sehe, dass der sehr kompetente Halbrecht die Funktion f₁ als die richtige identifiziert hat, mit der Begründung, dass f₂ durch den Punkt (1|1) geht.
Ich sehe hier aber kein Problem.
Bei x=1 hat die Funktion den Wert c⋅a. Da a<1 und c>1 sein soll, kann f(1) gegeben sein, wenn c=1/a gilt.
---------
* die Funktion würde dann so aussehen:
kurz und einfach :::::
egal welche Log-Fkt es auch ist ( ich meine welche Basis )
Alle gehen durch (1/0)
Denn Basis^0 ist gleich 1
So kommt nur f3 infrage
.
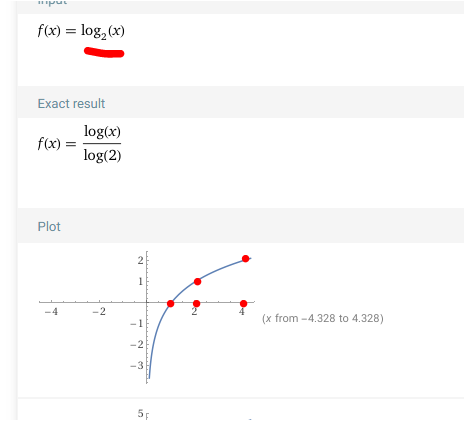
hier log2(x) , also zur Basis 2 .........mit den Punkten (1/0) , (2/1) und (4/2)

.
bei a < 1 , wird y immer kleiner je größer x wird
.
z.b a = 0.8
0.8^4 ist kleiner als 0.8^3
.
kommt nur 1,2 oder 5 infrage
.
c > 1 heißt vor allem positiv
bleiben 1 oder 2
.
Blau hat den Punkt (1/1)
bleibt nur f1
Was genau bedeutet eigentlich a, ist dass nur für positive negative Steigung? Y ist ja der Y-Achsenabschnitt soweit ich weiß
a ist nur ein Faktor , mehr nicht
und a soll hier halt kleiner 1 sein
also muss sowohl die Exponential und die Logarithmusfunktiion immer durch (1/0) gehen?