Ellipse im Rechteck?

Hat jemand eine Lösung und einen Lösungsweg?
3 Antworten
Hallo,
nach Wurzelziehung auf beiden Seiten bekommst Du die Funktionsgleichung
f(x)=Wurzel 0,5*(36-x²).
Da diese Funktion sowohl zur x-Achse wie auch zur y-Achse symmetrisch ist, reicht es, die Funktion im ersten Quadranten von 0 bis 6 zu betrachten.
Die Fläche des Viertelrechtecks ist x*f(x), also 0,5x*Wurzel (36-x²).
Diese Flächenformel leitest Du ab und setzt die Ableitung gleich Null.
Die Nullstelle dieser Ableitung und der Funktionswert, der herauskommt, wenn Du diesen Wert in die Funktionsgleichung einsetzt, ergeben die rechte obere Ecke des gesuchten Rechtecks.
Die anderen drei Ecken sowie Breite und Höhe ergeben sich dann aus den Symmetrieeigenschaften.
Mach Dir eine Zeichnung. Die Ellipse geht auf der x-Achse von -6 bis 6 und auf der y-Achse von -3 bis 3.
Zur Kontrolle: x0=Wurzel (18), f(x0)=0,5*Wurzel (18).
Herzliche Grüße,
Willy
Noch eine Skizze:
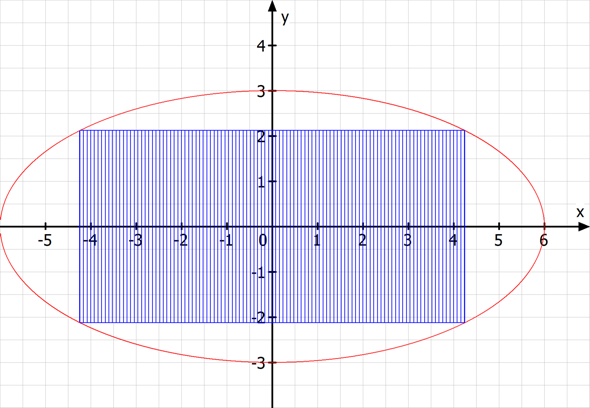
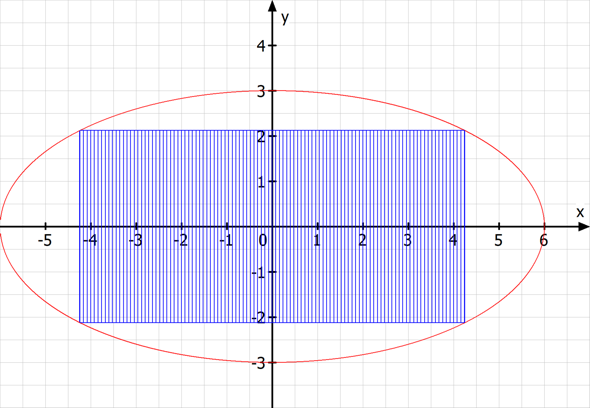
du brauchst nur das viertel rechteck im 1. quadranten zu maximieren;
breite = x
länge = y = 3/6 • wurzel(36-x²)
also
A = x • 3/6 • wurzel(36-x²) leitest du ab mit produkt- und kettenregel
A = 1/2 x • (36-x²)^1/2
A ' = 0
usw