Aus einer Geschwindigkeitsdifferenz und Zeit eine Strecke berechnen, wie geht das?
Ich habe 2 Geschwindigkeiten v, z.B. 140 km/h und 60 km/h, ebenfalls eine bestimmte Zeit t, 5 Sekunden, wie kann ich die Strecke aus der Geschwindigkeitsdifferenz und der Zeit berechnen, es geht hier um die Berechnung von der Bremsverzögerung(von 140 km/h zu 60 km/h abgebremst).
2 Antworten
Hallo Gfd123,
solche sog. "kinematischen" Aufgaben lassen sich immer mit demselben Werkzeugsatz aus nur drei Gleichungen berechnen. Von diesen drei Gleichungen würde die hier funktionieren s=1/2 a t² + v0 t +s0.
Die Beschleunigung a (hier: "negative Beschleunigung", oder Bremsverzögerung) beschreibt, wie stark sich die Geschwindigkeit pro Sekunde ändert. Du berechnest sie daher genau so, nämlich v2 minus v1, und das Ganze geteilt durch die Dauer (dieser Geschwindigkeitsänderung): (140-60)/5.
Allerdings musst Du die Einheiten aufeinander abstimmen. 3,6 km/h sind 1 m/s.
- Mit einer Beschleunigung von etwa minus 4,44 m/s²,
- einer Anfangsgeschwindigkeit v0 von 38,88 m/s,
- und einer Anfangsstrecke von s0 = 0m (weil in der Aufgabe nix von s0 drin steht)
wirst Du vermutlich eine Strecke von 138,9 m heraus bekommen.
Falls Dich die drei wichtigsten Gleichungen interessieren, findest Du hier noch ein 10-Minuten-Video, in dem sie gezeigt werden.
Ich vermute, du willst gleichmäßig bremsen (a=konst)?
Schau dir das Geschwindigkeits-Zeit-Diagramm (v-t-Diagramm) der Bewegung an. Der Graph der Geschwindigkeit ist eine fallende Gerade durch die Punkte (0s|140km/h) und (5s|60km/h) (die grüne Linie). Der zurückgelegte Weg s ist die Fläche unter dem Graphen von 0s bis 5s (bestimmtes Integral von v(t) nach dt von 0s bis 5s :-) (das ist die knalllila Fläche)
Diese Fläche hat die Form eines Trapezes und die kannst du geometrisch berechnen.
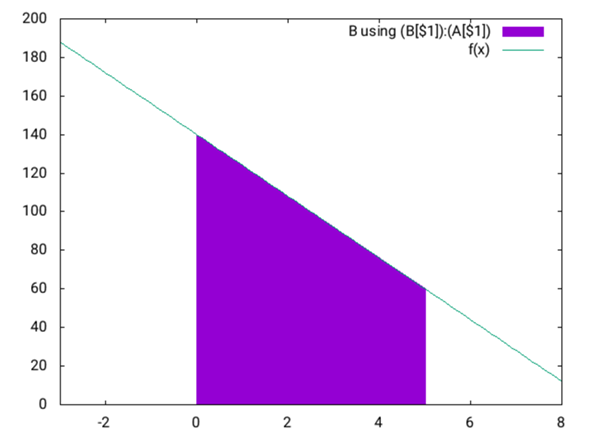
Wenn du das tust, wird dir auffallen, das du tatsächlich auch wie von @ludpin vorgeschlagen mit einer gleichförmigen Bewegung rechnen könntest, deren Geschwindigkeit der Mittelwert deiner beiden Geschwindigkeiten ist.
