Anordnung sechs gleich große Kreise in einem Kreis?
Wenn ich innerhalb eines Kreises sechs gleich große Kreise einzeichne. Ist dann immer Platz für ein siebter Kreis möglich?
- Wenn ja, wie lässt es sich mathematisch beweisen? Und wie lässt sich herrausfinden bei welcher anzahl an Kreisen ein weiteres automatisch Platz frei hat?
- Wenn nein, wie müsste ich die die Kreise anordnen dass kein siebter Kreis mehr hinein passt?
Ich weiss die Frage ist eher philiosophisch als praktisch...
Danke schon mal für Antworten
4 Antworten
Hallo Coldnez,
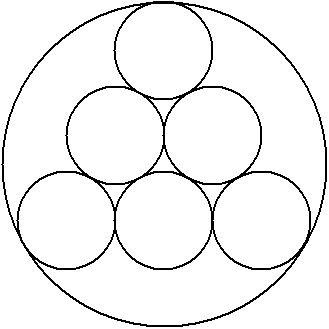
Du kannst sechs Kreise am platzsparendsten so anordnen, dass sie ein Dreieck bilden. Wenn Du den Umkreis dazu konstruierst, kannst Du feststellen, dass kein vollständiger siebter Kreis mehr hineinpasst, obwohl der große Kreis nach Flächeninhalt mehr als 10 mal größer ist.
Ich hänge Dir die Figur hier an.
Gruß Friedemann
Anschlußfrage: In welcher rechnerischen Relation stehen die kleinen zu dem großen Kreis?
Super, mit Bild ^^
Damit wäre die Frage beantwortet.
Zur Anschlussfrage, das werde ich auch noch berechnen.
@Rubenzahl2000
Die Position der Innenkreise ist beliebig. Der Aussenkreis muss kleinst-möglich sein ohne die Innenkreise zusammendrücken zu dürfen. Es wäre in dem Fall möglich, aber die Zwischräume erlauben dann ein weiterer Kreis. Ziel war es aber nur sechs in einem Kreis haben zu können - und nicht die kleinste Zwischenräume zu haben. Daher passt die Antwort zur Aufgabenstellung
Hallo Rubezahl2000,
Du hast recht. Meine Ausdrucksweise war falsch. Mit der Anordnung als Ring hat man aber sofort eigentlich 7 Kreise, und der Außenkreis hat dann genau den 3fachen Durchmesser, d.h. die 9fache Fläche eines kleinen Kreises.
Aber ich habe die Frage so verstanden, ob es eine Möglichkeit gibt, die sechs Innenkreise so anzuordnen, dass eben kein siebenter Kreis hineinpasst.
Gruß Friedemann
Wenn du Kreise in einem Kreis anordnest ist immer noch Platz für unendlich weitere Kreise. Zwischen den Kreisen entsteht ja wieder Ein Freiraum, wo ein weiterer Kreis hineinpasst.
Ich meinte aber GLEICH große Kreise. Die alle den größt-möglichen Platz in einem Kreis einnehmen. Den zwischenraum kann man irgendwann nicht mehr füllen. (Außer bei sechs Kreise?)
Es kommt drauf an wie groß du die einzelnen Kreise zeichnest. Solltest du davon ausgehen, dass alle sich schneiden, müsste gläubig ein 7. passen.
Ist leider nicht ganz klar, wie du dir das vorstellst.
Soll der 7. Kreis in die Mitte der 6 Kreise?
Mit Überschneidungen? Berührungen?
Und wie groß ist der große Kreis?
Die Kreise dürfen sich höchstens berühren, nicht überschneiden.
Stell dir dass so vor: Du zeichnest sechs gleich große Kreise auf einem Blatt, und dann den kleinst-möglichen Kreis der alle sechs Kreise miteinschließt, ohne Überschneidung oder auslassen von einem Kreis. Meine Theorie ist dann, das immer ein Platz frei ist, wo man ein weiteren Kreis einzeichnen kann, der genauso groß ist wie die anderen sechs. Und dieser Platz kann entweder in der Mitte oder am Rand sein oder sonst irgendwo innerhalb des Kreises. Und ich will wissen ob das stimmt.
Beispielsweise kann der große Kreis ein dreimal so großen durchmesser haben wie die sechs anderen, die dann alle mindestens zwei Berührpunkte haben. Im Prinzip ist es egal wie groß der große Kreis ist, hauptsache nicht zu klein für sechs Kreise. Und wenn sogar mehr wie sieben Kreise reinpassen, wäre der große unnötig groß
Wenn die 6 Kreise "im Kreis" (wie ein Ring) angeordnet werden, passen sie in einen "großen" Kreis hinein, der den 3-fachen Durchmesser hat wie die kleinen Kreise. Und in der Mitte ist dann noch Platz für den 7. Kreis.
Hier ein Bild dazu: http://www.paranormal.de/paramirr/geo/z8.gif
Du kannst genau sieben Kreise einfügen, jeder ein Drittel von dem Außenkreisdurchmesser. Dabei ist einer von den kleinen Kreisen konzentrisch in der Mitte, die anderen 6 um den Kreis in der Mitte, sie berühren alle den Außenkreis innen und den kleinen Kreis in der Mitte aussen.
Bist du sicher, dass das die platzsparendste Anordnung ist?
Wenn die 6 Kreise "im Kreis" (wie ein Ring) angeordnet werden, passen sie in einen kleineren Kreis hinein, als in deiner Konsrtuktion.