Analysis mathe wann ableiten?
Hallo,
warum muss ich bei folgender Aufgabe ableiten? Und hilft mir die Gerade dabei?
Aufgabe:
Die Abbildung zeigt das Schaubild der Funktion f. Ermitteln Sie einen möglichen Funktionsterm.
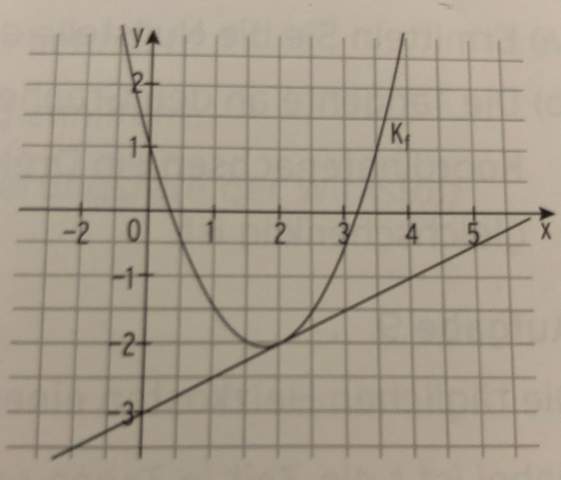
Danke für die Hilfe
Lg
3 Antworten
Hier handelt es sich offensichtlich um eine Parabel, deren allgemeiner Ansatz lautet:
f(x) = ax^2 + bx + c
Wir haben 3 Parameter a, b und c, die wir lösen müssen und um 3 Unbekannte zu lösen brauchen wir 3 Informationen. Die haben wir auch:
1) f(0) = 1
2) bei x = 2 hat die Parabel die eingezeichnete Tangente mit der Steigung m = 1/2:
f'(2) = 0,5
3) Der Scheitelpunkt einer Parabel liegt immer genau zwischen den beiden Nullstellen. Das wäre hier bei x = 1,75:
f'(1,75) = 0
Da sich zwei Informationen auf die Steigung beziehen, müssen wir ableiten:
f'(x) = 2ax + b
Da setzen wir Info 3) ein:
f'(1,75) = 2*1,75*a + b = 0
3,5a * b = 0 (Gl. 1)
Info 2) eingesetzt:
f'(2) = 2*2*a + b = 0,5
4a + b = 0,5 (Gl. 2)
Nun rechnen wir Gl.1 - Gl.2:
-0,5a = -0,5
a = 1
in Gl. 1 eingesetzt:
3.5 + b = 0
b = - 3,5
Damit lautet die Funktion:
f(x) = x^2 - 3,5x + c
Da setzen wir Info 1) ein:
f(0) = 2*0^2 - 3,5*0 + c = 1
c = 1
Also lautet das Ergebnis:
f(x) = x^2 - 3,5x + 1
Zur Probe gebe ich die Funktion in einen Funktionsplotter ein:
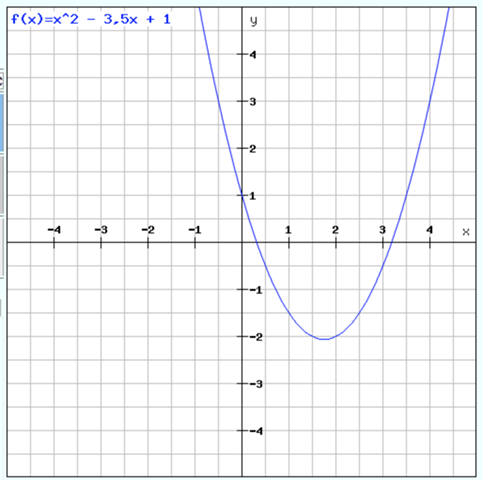
..und siehe da, das haut hin.
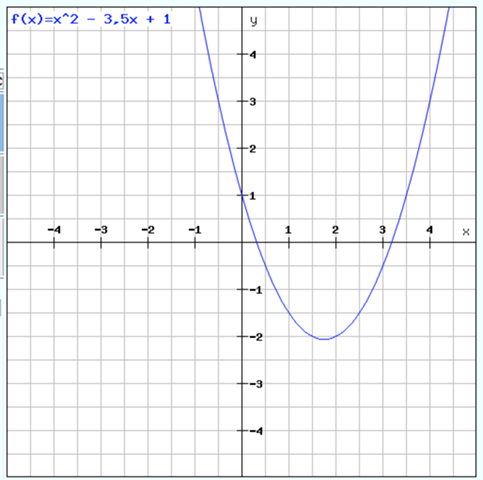
Ich nehme an, die Parabel soll die Funktion sein, deren Funktionsterm du ermitteln sollst.
Dinge du du weißt :
f(0) = 1
f(7 / 2) = 1
Es gibt eine Tangente, die mit der Funktion einen Punkt gemeinsam hat.
Diese Tangente geht durch die Punkte
P(0 | - 3)
P(3 | - 1.5)
P(4 | - 1)
P(5 | - 0.5)
Deshalb lautet die Tangente y = (1 / 2) * x - 3
Nun zum Lösungsweg :
f(x) = a * x ^ 2 + b * x + c
Aus f(0) = 1 folgt sofort c = 1 sodass sich f(x) ändert zu :
f(x) = a * x ^ 2 + b * x + 1
f´(x) = 2 * a * x + b
Nun stellst du ein Gleichungssystem auf :
Mit f(7 / 2) = 1 ergibt sich :
I.) a * (7 / 2) ^ 2 + b * (7 / 2) + 1 = 1
I.) (49 / 4) * a + (7 / 2) * b = 0
Die Tangente y = (1 / 2) * x - 3 hat mit der Parabel f(x) einen Berührpunkt (x_t | y_t)
Daraus folgt :
y_t = (1 / 2) * x_t - 3
und
y_t = a * x_t ^ 2 + b * x_t + 1
Die Parabel hat im Berührungspunkt die Steigung der Tangente, daraus folgt :
f´(x_t) = 1 / 2
2 * a * x_t + b = 1 / 2
Der Übersichtlichkeit wegen fasse ich das komplette Gleichungssystem noch einmal zusammen :
I.) (49 / 4) * a + (7 / 2) * b = 0
II.) y_t = (1 / 2) * x_t - 3
III.) y_t = a * x_t ^ 2 + b * x_t + 1
IV.) 2 * a * x_t + b = 1 / 2
Dieses Gleichungssystem musst du lösen und erhältst unter Umständen mehrere Lösungen. Anhand des Bildes kannst du aber erkennen welche Lösung es ist :
a = 1
b = - 7 / 2
x_t = 2
y_t = - 2
Außerdem wusste man bereits, dass c = 1 ist.
Also erhält man wegen f(x) = a * x ^ 2 + b * x + c jetzt :
f(x) = 1 * x ^ 2 - (7 / 2) * x + 1
lässt sich noch vereinfachen :
f(x) = x ^ 2 - (7 / 2) * x + 1
Der Berührpunkt zwischen Tangente und Parabel lautet (2 | - 2)
Die Ableitung hilft Dir, den Scheitelpunkt der Kurve zu berechnen, oder denjenigen Punkt, an welchem eine bestimmte Steigung vorliegt. Denn die Ableitungsfunktion der Kurve yS=f'(xS) ist im Scheitelpunkt P(xS,yS) gleich 0.
So wie die Aufgabe aussieht, geht die Gerade entweder durch den Scheitelpunkt der Kurve durch, oder berührt die Kurve irgendwo kurz nach dem Scheitelpunkt.
Leider ist die Grafik etwas unscharf und man sieht nicht, welcher von beiden Fällen vorliegt. Ich hätte jetzt auf das mit dem Scheitelpunkt schneiden getippt (was nicht richtig ist, wie sich weiter unten herausstellt...)
Die Gerade scheint die Funktion g(x)=0.5x - 3 zu haben. D.h. die Steigung der Geraden wäre 0.5. (Lineare Funktion, Typ y=mx+q, wobei m die Steigung ist).
Die Kurve scheint die Funktion f(x)=x^2 - 3.5x + 1 zu haben. Die Ableitung davon wäre f'(x)=2x - 3.5
Wenn man das nach null auflöst:
2x - 3.5 = 0
2x = 3.5
x=1.75
somit xS=1.75 und yS = f(xS) = f(1.75) = 1.75^2-3.5*1.75 + 1 = -2.0625
also liegt der Scheitelpunkt P bei (1.75/ -2.0625).
Der Schnittpunkt von f(x) und g(x) liegt dort, wo f(x) = g(x)
also kann man folgende Gleichung aufstellen:
x^2-3.5x+1 = 0.5x-3
Als Lösung für x erhalten wir den Wert 2. Setzen wir 2 im Term ein, erhalten wir die y-Koordinate des Schnittpunkts, die ebenfalls 2 beträgt.
Der Schnittpunkt (Q) ist also: Q (2 / 2).
Somit wissen wir nun auch, trotz unscharfem Bild, dass die Gerade die Kurve nur berührt, aber nicht im Scheitelpunkt schneidet, denn Punkte P und Q sind offensichtlich unterschiedlich.
Zum Prüfen, ob das Resultat stimmt, können wir noch die Ableitungen beider Funktionen im Punkt Q ausrechnen. Die Steigungen dort müssten die selben sein:
f'(x)=2x-3.5 g'(2)=0.5 (g'(x) hängt nicht mehr von x ab und ist immer 0.5!)
f'(2)=2*2-3.5 = 0.5 was mit dem Wert von g'(x) übereinstimmt.