[Mathe] Monotonie bestimmen?
Guten Abend,
vielleicht mag mir ja jemand bei den folgenden Aufgaben helfen. Ich habe alles was ich zu den Aufgaben weiß unter das Bild geschrieben. :-)
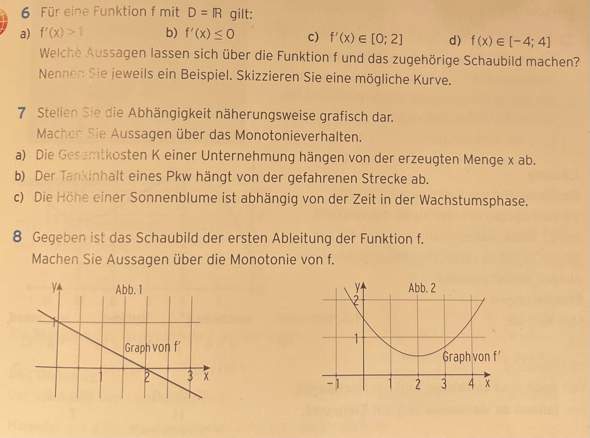
Hier würde ich folgendes schreiben:
a) Die Funktion ist streng monoton wachsend
b) Die Funktion ist monoton fallend
Die Aufgabenteile c) und d) verstehe ich noch nicht.
Aufgabe 7So eine Art von Aufgabe habe ich noch nicht gemacht und ich verstehe sie leider noch nicht so wirklich.
Aufgabe 8Hier würde ich folgendes schreiben:
Abbildung 1:
Die Funktion ist streng monoton fallend
Abbildung 2:
Die Funktion ist monoton fallend von (-unendlich; 2] und monoton steigend von [2; unendlich).
4 Antworten
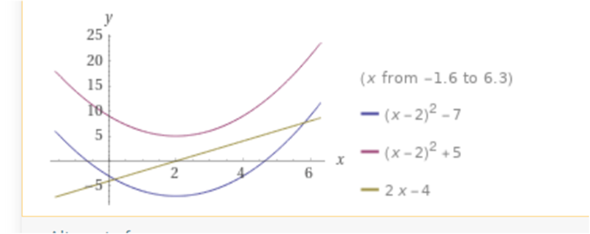
Aufgabe 6)
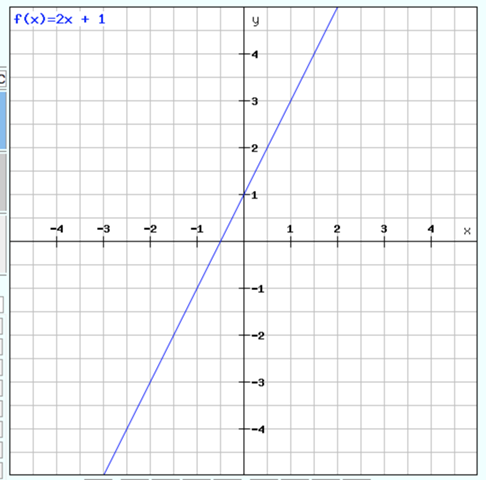
a) Die Steigung ist für die gesamte Funktion größer als 1. Das bedeutet, die Funktion ist streng monoton steigend. Hier kommt keine Polynomfunktion in Frage, da deren Graphen regelmäßig einen Hoch- Tief- oder Wendepunkt mit f'(x) = 0 besitzen.
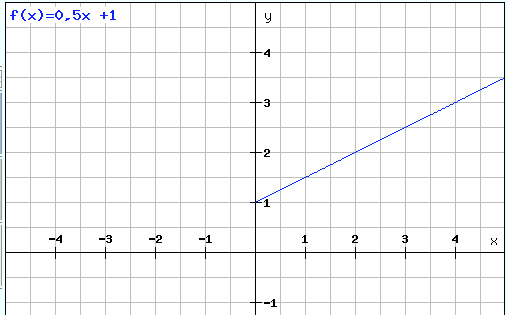
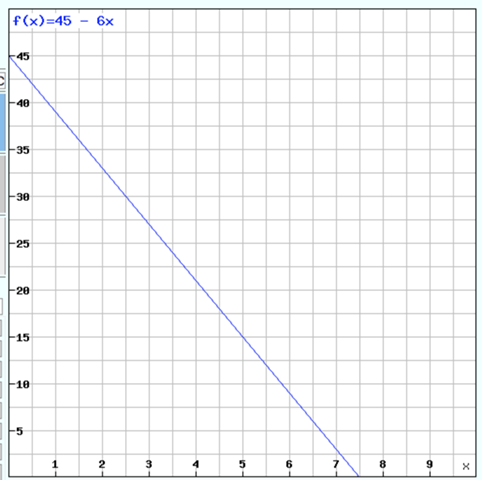
Beispiel: Gerade mit m = 2:
y = 2x +1
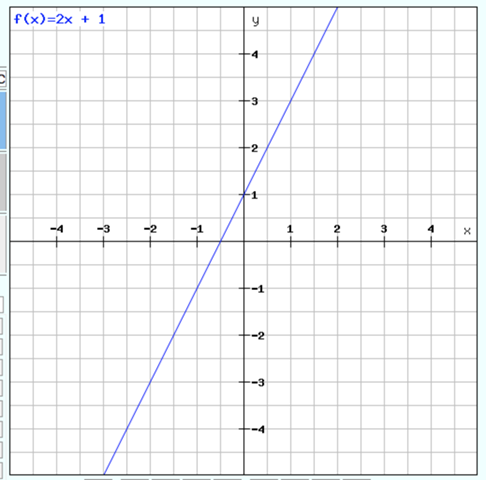
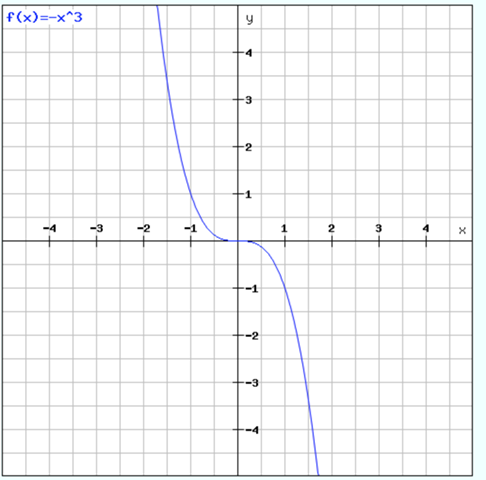
b) Die Steigung ist 0 oder negativ. Der Graph könnte einen Wendepunkt mit waagrechter Tangente haben, aber keine Extremstelle. Damit f'(x) stets negativ bleibt, muss f'(x) ausschließlich gerade Potenzen enthalten und negativ sein. Als Funktion käme ein Polynom 3. Grades oder eine e-Funktion in Frage. Eine solche Funktion wäre im gesamten Defintionsbereich monoton fallend.
Beispiel: f(x) = -x^3
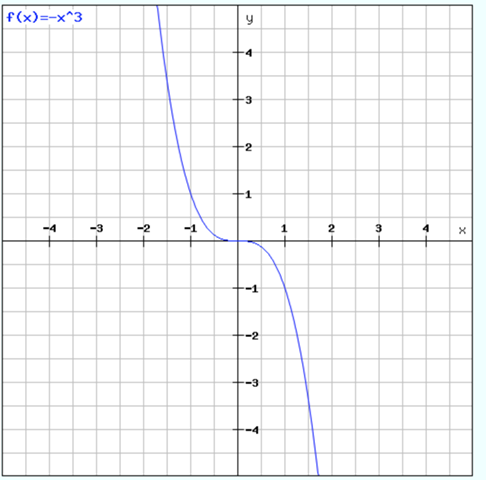
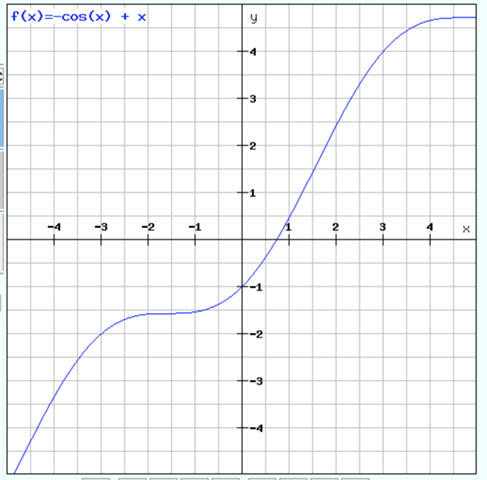
c) Die Steigung bewegt sich zwischen 0 und 2. Sie liegt immer im positiven Bereich. Eine solche Funktion wäre monoton steigend, aber nicht streng monoton steigend, da eine waagrechte Tangente möglich ist.
Typische Funktionen, die sich zwischen zwei Werten bewegen sind die trigonometrischen Funktionen. So könnte f'(x) = sinx + 1 sein, womit sich f'(x) genau im angegebenen Intervall bewegt.
mit f'(x) = sinx + 1
wäre
f(x) = -cos(x) + x
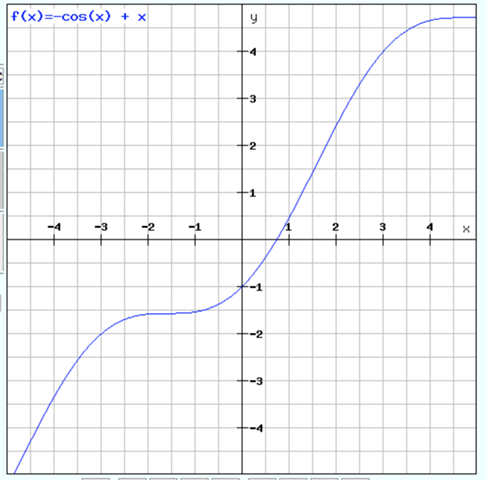
Ach, Aufgabe d) hab ich ganz vergessen.
d)
Über die Monotonie dieser Funktion lässt sich nichts konkretes sagen. Wenn der Funktionswert sich im genannten Intervall bewegen soll, kommt wieder eine Trigonometrische Funktion in Frage, z.B.
f(x) = 4* sin(x)
Die Funktion hat also abwechselnd steigend und fallende Abschnitte.
Ich habe noch eine Frage zu deiner Antwort zu c):
So könnte f'(x) = sinx + 1 sein, womit sich f'(x) genau im angegebenen Intervall bewegt.
mit f'(x) = sinx + 1
wäre
f(x) = -cos(x) + x
Das die Funktion f(x) = - cos(x) + x eine passende Funktion ist, habe ich verstanden. Aber das davor, mit f‘(x) = sin (x) + 1 verstehe ich nicht, was du damit meinst und warum das so ist. 🤔
Der sin(x) schwankt zwischen -1 und +1. Das müssen wir um 1 anheben, damit daraus 0 bis 2 wird.
Bei d) gehen wir auch von sin(x) aus. Um das ins Intervall einzupassen, nehmen wir einfach das 4-fache.
Bei c) istdas Intervall für f' und bei d) das Intervall für f(x) angegeben.
Ich habe es verstanden! Unglaublich! Ich dachte, da die Funktion ja an manchen Stellen negativ ist, es dann ja nicht passt. Aber es handelt sich ja um die abgeleitete Funktion und wenn man einen x-Wert einsetzt hat man die Steigung an der Stelle des x-Wertes. - LOGISCH 😊 Meine Verknüpfungen im Gehirn werden immer mehr
Brauchst du Aufgabe 8 auch noch? Die ist im Vergleich zu den vorherigen eher einfach.
Kurz:
streng monton steigend: (-∞; 2)
streng monoton fallend: (2; ∞)
b)
Da f'(x) stets positv ist, ist f(x) streng monoton steigend.
Brauche ich nicht, vielen vielen Dank 😅
Aber ich hätte noch eine Frage zu einer Aufgabe, die ich vorhin versucht habe:
“Für die zweite Ableitung der Funktion f gilt f‘‘(x) = 1 - 2x. Das Schaubild von f verläuft durch den Ursprung mit Steigung 2. Bestimmen Sie f(x).“
Ich weiß, dass man, wenn man integriert und eine gewisse Funktion bestimmen muss „+c“ hinten dranhängen muss. Aber hier muss ich ja zweimal aufleiten. Suche ich mir dann einfach einen zweiten Buchstaben aus? Wie wird dann das bereits stehende „+c“ vom ersten aufleiten behandelt?
Die Bedingungen die gegeben sind sind mir auch klar:
f(0) = 0
f‘(0) = 2
Suche ich mir dann einfach einen zweiten Buchstaben aus?
oder du nimmst c1 und c2. Aber du musst bei jedem Aufleiten die Konstante ergänzen, sonst krigest du womöglich nicht die Bedingungen erfüllt.
Die Lösung lautet
f(x) = -1/3*x^3 + 1/2*x^2 + 2x
Bei d) steht ja nicht die erste Ableitung da sondern die normale Funktion.
Heißt das, dass die Funktion den Bereich [-4;4] nicht verlassen darf?
Richtig...und zwar im gesamten defintionsbereich von R. Das geht nur trigonometrisch.
Also kann ich z.B. x = 1 als Funktion nehmen? Du hast dich mit f(x) = 4* sin(x) in der Aufgabe verlesen, oder?
x = 1 ist keine Funktion, sondern eine Parallele zur y-Achse.
Du hast dich mit f(x) = 4* sin(x) in der Aufgabe verlesen, oder?
Bei Aufgabe 6d) ?
nein, das ist die Lösung.
Aber in der Aufgabe 6 d) steht ja die normale Funktion und nicht die erste Ableitung. Kannst du mir das nochmal erklären? f(x) e [-4;4]
Ja, das ist das verflixte daran, dass einmal f'(x) genannt wird, aus dem man direkt Aussagen über die Monotonie ableiten kann und einmal in d) aber nur f(x) genannt ist. Da kann man keine direkten Aussagen zur Monotonie machen. Da muss man sich zuerst überlegen, welche Funktion das Intervall [-4;4] ausfüllen kann.
Funktionen mit einer oberen und unteren Grenze über den gesamten Defintionsbereich R sind typischerweise Schwingungen, also trigonometrische Funktionen. Die Grundfunktion jeder Schwingung ist f(x) = sin(x). Die hat aber nur eine Amplitude von -1 bis +1. Also muss man die Amplitude vervierfachen, damit sie das Intervall [-4;4] bedient.
Wenn man nun also als Beispiel f(x) = 4sin(x) wählt, also die einfachste aller Möglichkeiten, muss man aus der Funktion selber auf die Monotonie schließen. Bei einer Sinusschwingung wechseln sich Hoch- und Tiefpunkte periodisch ab und damit ändert sich auch das Monotonieverhalten periodisch.
Ich hoffe, das war verstänbdlich, sonst hake solange nach, bis es "klick" macht.
Ich dachte, dass die Werte im Intervall x-Werte sind und sich die Funktion nur innerhalb des Bereiches [-4;4] bewegen darf
Ahh..jetzt sehe ich den Knoten in deinen Hirnwindugen:
Das steht nicht x ∈ [-4;4], also der Defintionsbereich.
Der Defintionsbereich steht oben in der Aufgabe: D = ℝ
Das steht f(x) = [-4;4] und das gibt den Wertebereich an, also den y-Wert, den die Funktion einnehmen kann.
Magst du dir noch die Antwort mit einer Frage von mir (Auf die Hauptfrage) anschauen? :-) Er sieht genau so aus wie ein Kommentar von jedem, der antwortet. Müsste etwas weiter unten sein 😊
Aufgabe 7)
a)
Wenn der Zusammenhang linear ist, steigen die Kosten proportional zur Produktiuonsmenge. Der Graph wäre damit eine Gerade mit positiver Steigung und damit streng monoton steigend. x-Werte sind nur positiv, da es eine negative Produktion nicht gibt.
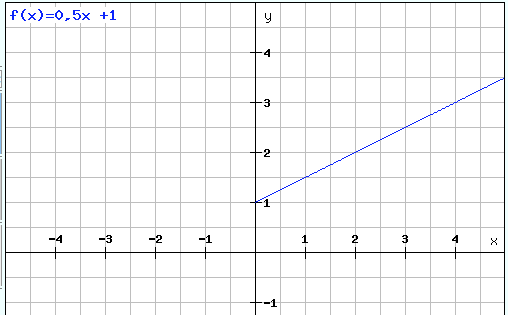
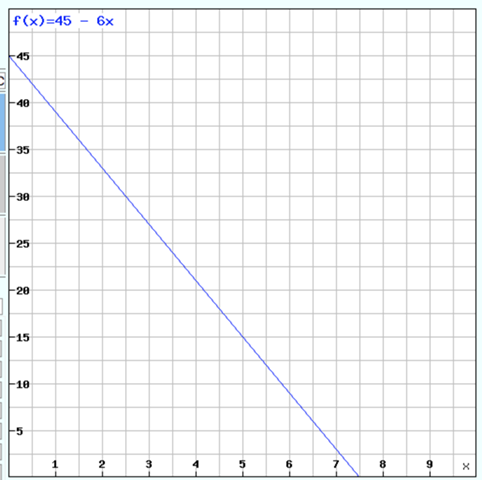
b) Je weiter das Auto fährt, umso leerer wird der Tank. Die Funktion ist also streng monoton fallend. Das Auto fährt mit vollem Tank los, bis er leer ist. x für die Fahrtstrecke in 100 km und y für den Tankinhalt in Liter sind immer positiv.
c) Die Höhe der Sonnenblume nimmt während der Wachstumsphase nur zu und nicht ab (solange sie niemand abschneidet). Die Funktion ist also monoton steigend, wobei es zeitweise bei ungünstigen Bedingungen auch kein Wachstum geben kann. Daher ist die Funktion nicht zwingend streng monoton steigend.
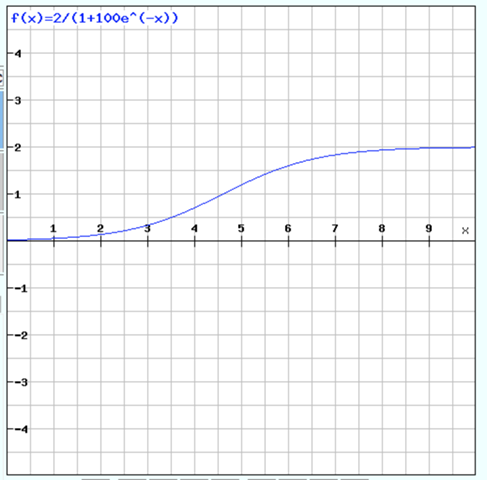
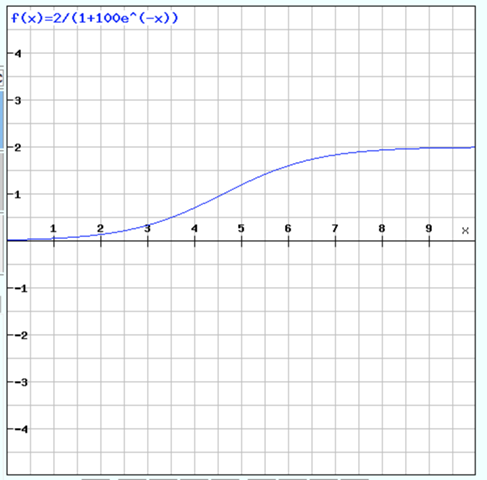
Eine typische Wachstumsfunktion ist die e-Funktion, z.B.
f(x) = 2/(1+100e^(-x))
x = Zeit in Wochen
y = Höhe in Meter
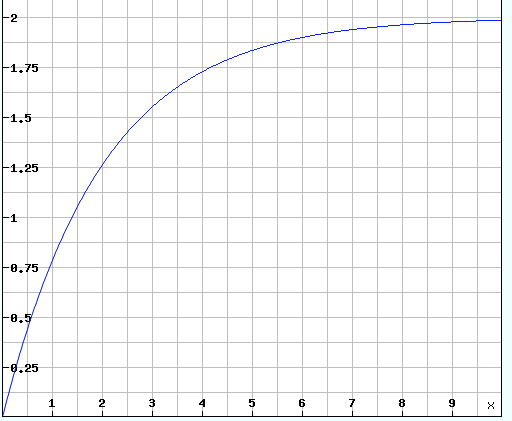
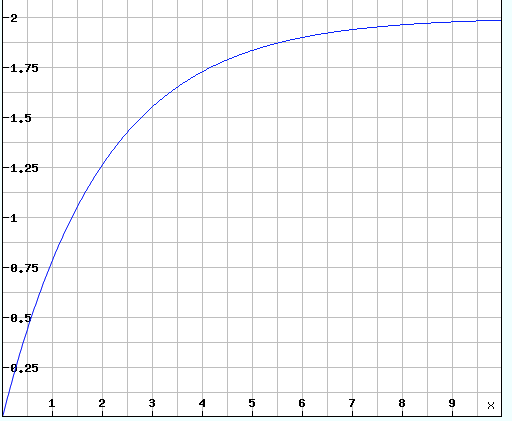
Aber auch so ein Wachstum wäre denkbar:
6a)
ok
f'(x) > 1 heißt , sie hat keine Nullstellen ,daher bei f(x) keine Extrema.
.
6b)
????
f(x) = -(x-2)^4 hat bei x = 2 einen Hochpunkt
bis 2 wachsend , danach fallend.
.
c und d habe ich erstmal keinen Plan .
Eine Fkt deren y-Werte auf ein Intervall begrenzt ist ?
da käme mir nur sinus , cosinus in den Kopf
.
.
8)
bis 2 pos Stei
ab 2 neg Stei
.
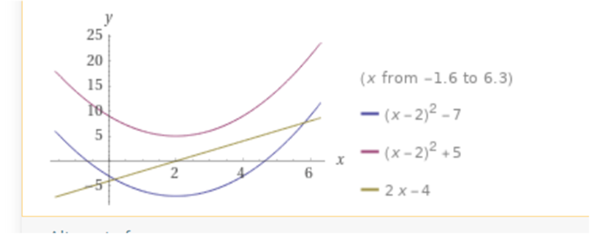
typischer Fall von Parabel
Scheitelpunkt bei 2
.
Und 7 ?
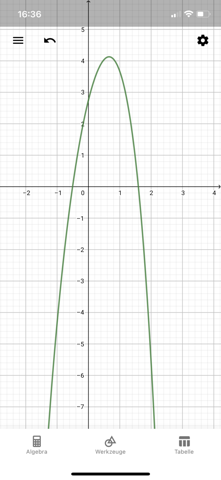
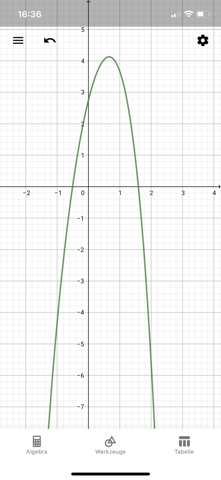
Hat jemand Lust, hier kurz zu schauen, wo ich einen Fehler gemacht habe? :-) Das Schaubild geht nicht durch die Punkte bei mir.


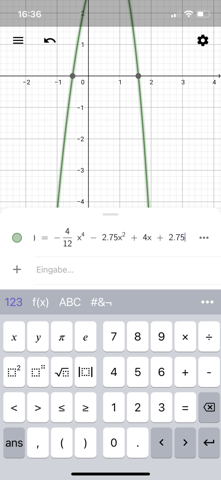


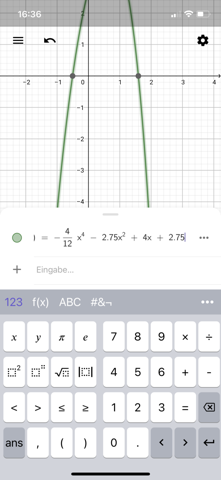
P(3/-7) dritte Zeile:
was gibt -27 + 12?
Sollte das zufällig -15 und nicht + 15 ergeben, ergibt sich b = 2 ; c = -1 und dann klappts auch mit den Punkten.
Leichtsinnsfehler sind die ärgerlichsten. In meiner letzten Mathe Arbeit habe ich eine 1,0 geschafft 😅 Freitag die nächste und letzte Arbeit vor den Prüfungen. Bald bin ich endlich durch mit der Schule 🏫
Wenn du magst kannst du dir auch die Frage gerne anschauen anschauen, falls du noch Lust hast. Ich bin Dir unendlich dankbar… Tut mir leid für die vielen Fragen im Moment 😬
(Aufstellen von Kurvengleichungen; maximal lineares Gleichungssystem mit 2 Zeilen -> und ich weiß nicht, ob ich damit die Kurvengleichungen aufstellen kann, mit nur 2 Zeilen LGS (was wir können müssen, aufgrund von Corona dieses Schuljahr nur 2 statt 3 Zeilen))
https://www.gutefrage.net/frage/mathe-hilfe---funktionsterm-mithilfe-abbildung-aufstellen
Gehe auf ein Berufskolleg (mache die Fachhochschulreife) und bin in der 12. Klasse (letzte Klasse) - schreibe im Mai die Abschlussprüfungen in Deutsch, Mathe, Englisch und Betriebswirtschaftslehre
Ok, die Prüfungen fürs Abschlusszeugnis sind natürlich enorm wichtig....heutzutage zählt ja vor allem die Papierform, die jemand vorzeigen kann.
Vielen vielen Dank 🙏 Am Freitag schreibe ich die letzte Klassenarbeit und dann steht hoffentlich meine Anmeldenote für die Prüfung mit einer 1 da… Lernen zahlt sich aus. Ich danke dir für die unendlich wertvolle Hilfe 💚