Ableitungsfunktion zeichen?
Moin,
ich habe bei der dritten Aufgabe ein kleines Problem
Wie zeichnet man den Graphen der Ableitungsfunktion bei der zweiten Funktion? Ich sehe dort nur einen Tiefpunkt an der Stelle 0 und bin unsicher, wie ich den Graphen entsprechend zeichnen soll.

Vielleicht ergibt sich daraus ja auch gleich die Antwort auf die Frage weiter unten: „Was folgt aus der Achsensymmetrie des Graphen?“
ich bedanke mich im Vorraus für eure Antworten
2 Antworten
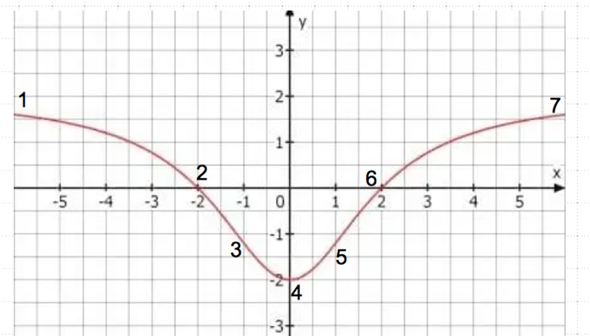
Als erstes analysieren wir den Graphen, dazu markiere ich die wichtigsten Punkte:

1: Steigung leicht negativ, geschätzt -0,1
2: Steigung etwa 1
3: Wendepunkt mit der stärksten Steigung (Betrag), geschätzt -1,5
4: Steigung 0
Jetzt aus Symmetriegründen:
5: +1,5
6: +1
7: + 0,1
Die Punkte zeichnest du ins Koordinatensystem und verbindest sie.
Umgekehrt könnte auch die Frage weiter unten zur Lösung der oberen Frage beitragen.
Habt ihr das nie ausgerechnet?
(1)
f gerade (achsensymmetrisch zur y-Achse):
f(-x) = f(x)
Kettenregel:
f'(-x) = -f(x)
also f'(x) ungerade (punktsymmetrisch zum Ursprung)
(2)
f ungerade
f(-x) = -f(x)
Kettenregel:
f'(-x) = +f(x)
also f'(x) gerade
Die Steigung der Funktion f(x) geht gegen 0 für x gegen ±unendlich. Damit ist das Verhalten von f'(x) dort schon mal klar.
f(x) hat ein Minimum - das hast du schon bemerkt.
f(x) hat zwei Wendepunkte.