Mathematik Prisma?
Wie geht Aufgabe B ich bitteum hilfe und wie kann ich heraus finden wie lang die Höhe ist…
Danke!

3 Antworten
hier ist das Dreieck für die Höhe

.
Höhe ist laut meiner Rechnung zwischen 10.80 und 11.00 cm
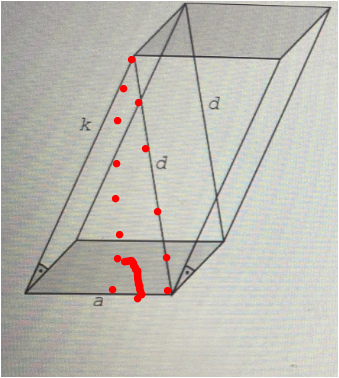
die Höhe ist die andere Kathete , das was gesucht ist .
Gegeben die Hypo und eine Kathete
d² = h² + (a/2)²
Guten Nacht,
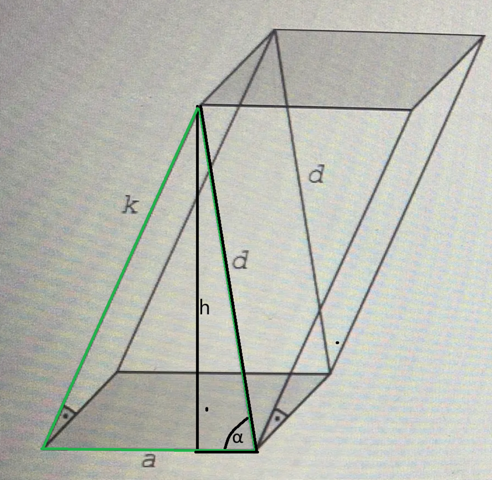
Erstmal habe ich eine Zeichnung gemacht.

Nenne den Winkel zwischen a und d einfach (α). Und nenne die Höhe des Primas h. Dies habe ich mit schwarz angegeben in dem Bild.
Wir fangen an mit dem grünen Dreieck. Weil k, d und a bekannt sind, kann man α einfach ausrechnen mit dem Cosinusregel. Laut Cosinusregel: k² = d² + a² - 2*d*a * cos(α). Also cos(α) = (k² - d² - a²) / (-2*d*a) = (11² - 11² - (3,5)²) / (-2 * 11 * 3,5) = (-12,25 / -77) = (12,25 / 77). Und α = cos-1(12,25 / 77) = 80,84...°
Nun zum schwarzen Dreieck. α und d sind bekannt, also kann h einfach berechnet werden. sin(α) = h / d -> h = d * sin(α) = 11 * sin(80,84...°) = 10,8599.... cm
Und dann ist V = 3,5 * 3,5 * 10,8599... = 133,03 cm³. Also das stimmt überein mit dem Antwort.
Mit freundlichen Grüßen
Tijn
Das Dreieck mit den Seiten k, d und a ist ein gleichschenkliges Dreieck. Die Seiten k und d sind gleich lang und a ist die Grundseite. Die Höhe dieses Dreiecks kannst du ganz einfach mit Pythagoras berechnen.
Schau dir das von Halbrecht ergänzte Bild an.
Die Höhe beträgt 10.86 cm
Wie kann ich herausfinden wie lang die Höhe ist? Wel ich weiss ja kich wie lang die andere Kathete ist bei a? Oder geht das irgendwie?
Die Höhe bei einem gleichschenkligen Dreieck teilt doch die Grundseite genau in der Mitte. Du hast also k oder d als Hypotenuse und a/2 als Kathete. Und h ist die zweite Kathete.
weil du weisst ja dann nich wie lang die andere Kathete bei a ist oder schon?