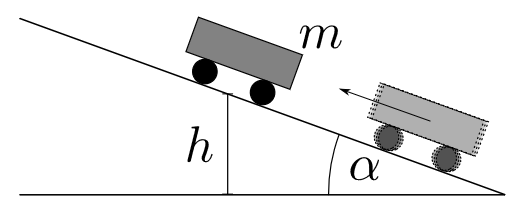
Schiefe Ebene mit Rollreibung?
Eine Ära geht zu Ende - nach 42 Jahren lief gestern die allerletzte Ausgabe "Wetten daß?!". Doch unser "Experimentalphysk 1" und "Plasmaphysik"-Professor denkt nicht im Traum daran aufzuhören. Viel eher beglückt er uns dieses Wochenende mit folgender Aufgabe: Ein Wagen der Masse m = 30 kg habe eine Anfangsgeschwindigkeit v0 = 15 m/s und rolle von unten eine schiefe Ebene mit einem Anstellwinkel von α = 10◦ nach oben a) Welchen Weg s legt der Wagen bis zum Stillstand zurück, und welche Höhe erreicht er dabei? Wir gehen von einer reibungsfreien Bewegung aus. b) Zeige mittels den Bewegungsgleichungen, dass die erreichte Höhe unabhängig vom Anstellwinkel α und der Masse m des Wagens ist. Ist die benötigte Zeit bis zum Stillstand auch unabhängig von dem Winkel und der Masse? c) Nun berücksichtigen wir eine Rollreibung von μ = 0,05. Welche Höhe erreicht der Wagen nun? Ist die erreichbare Höhe immer noch unabh¨angig vom Anstellwinkel und der Wagenmasse? Jensek81'scher Ansatz: a) Epot = Ekin mgh = 1/2 m v0² | geteilt durch mg h = 1/2 m vo² / mg = 1*mvo² / 2 * mg = v0² / 2g = (15m/s)² / 2 * 9,81 m/s = 11,47 m Weg: sin α = h/s | geteilt durch s sin α * s = H | geteilt durch sin α s = h / sin α = 11,47m / sin (10◦) = 66,05 m b) Da h = v0² / 2 g ist die Höhe von der Geschwindigkeit abhängig, aber nicht von Anstellwinkel α und Mase. Fr = Fg * sin ◦ = mg * sin ◦ s = 1/2 a t² + v_0 * t a = -Fh/M s => s = 1/2 (-Fh/M) t² + v_0 * t = - Fh/M t + vo Fh/m t = v0 | geteit durch Fh/m => t = v0m/Fh = (vo * m) / (m * g * sin α) = vo/ (g * sin α) => abhängig von Winkel α, aber Masse kürzt sich raus. c) E_gesamt = Epot + E_kin - Reibungsarbeit 1/2 m v² = m g h + 1/2 m v0 ² - μ * FN * s 1/2 m v² = ( m g h + 1/2 m v²- μ * m * g * s 1/2 m 0² = g h + 1/2 v0 - μ * g * s 0 = g * h + 1/2 v0 - μ * g * s | + μgs g h + 1/2 v0 = μ g s | - 1/2 0 gh = μgs - 1/2 v0 | g h = (μgs - 1/2 v0 ²) / g h = (0,05 * 9,81 m/s - 66,05 m - 1/2 * 15 m/²)/(9,81 m/s) und da kommt 'ne negative Höhe raus. Und das macht mich fertig... Jensek81'sche Grüße, Jesek81