Woran kann man erkennen, ob es zwei, ein oder kein Schnittpunkt gibt?
Was bzw wie muss man rechnen um zu sehen, dass es keinen oder zwei oder einen Schnittpunkt gibt? Danke im Voraus
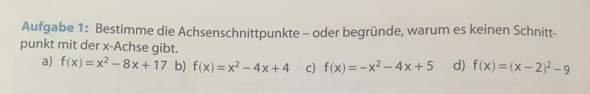
Also mit der x-Achse
4 Antworten
Es handelt sich durchweg um Parabeln, bzw. um quadratische Gleichungen. Entweder liegen sie über oder unter der x-Achse oder sie berühren sie oder sie schneiden sie zweimal.
Dazu kann man einfach schauen, für welche x der Funktionswert 0 ist. Gibt es da zwei Lösungen, gibt es auch zwei Schnittpunkte. Gibt es nur eine Lösung, berührt die Parabel die x-Achse an nur einem Punkt. Gibt es keine Lösung, so gibt es auch keinen Schnitt- oder Berührungspunkt mit der x-Achse.
Beispiel:
Schauen wir, wo die Funktion 0 ist, wo sie also die x-Achse berührt oder schneidet:
Dies ist eine quadratische Gleichung, die mit der pq-Formel gelöst werden kann:
Quadratische Gleichung in Normalform:
wird gelöst mit der pq-Formel:
Für das Beispiel ergibt sich:
In diesem Fall ist unter der Wurzel eine negative Zahl da 16-17 = -1 ist. Daher gibt es hier keine Lösung also auch keinen Schnittpunkt mit der x-Achse.
Den Funktionsterm =0 setzen und diese Gleichung nach x auflösen.
Wenn du richtig rechnest, dann siehst du ja, ob es eine oder zwei oder gar keine Lösung gibt.
bei
f(x) = x² + bx + c
berechnest du die Diskriminante D
(-b/2)² - c
bei a)
(8/2)² - 17 = 16-17 = -1 also keine Nullstelle (weil D<0)
wenn D=0 dann eine Nullst.
wenn D>0 dann 2 Nullst.
Man könnte ganz einfach die Nullstellen berechnen. Dann weiß man, ob und wie viel es gibt.
Oder man bestimmt den Scheitelpunkt. Wenn man dessen Lage (oberhalb, auf oder unterhalb der x-Achse) und das Wissen, ob die Parabel nach oben oder unten geöffnet ist verbindet, kann man auch sagen, ob und wie viel Nullstellen es gibt.
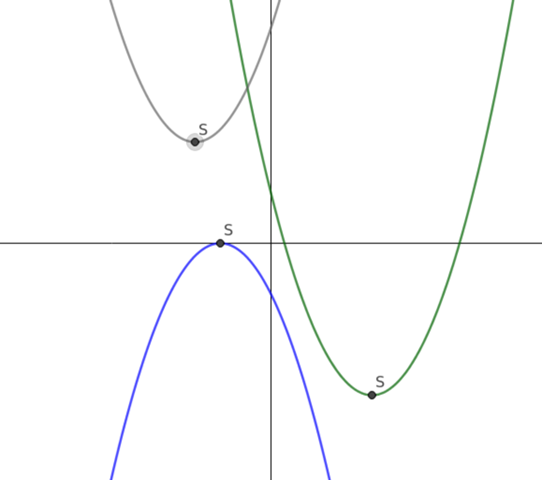
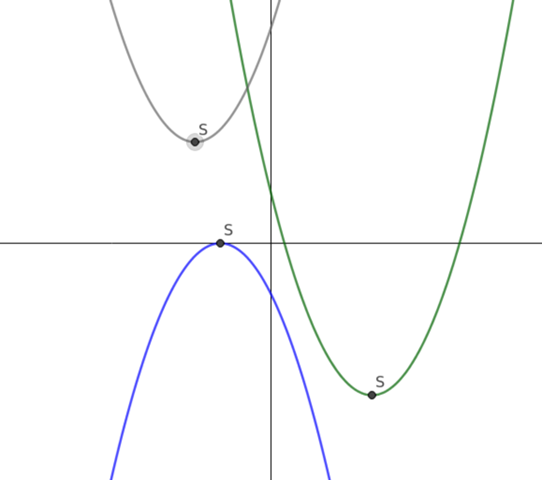
Vielen Dank! Aber der y-Wer ist bei a) 17 oder? Also S (0|17)?