Woran erkennt man ob eine gerade steigt oder sinkt?
Hallo, Ich würde gerne wissen woran man erkennt ob eine gerade steigt oder sinkt
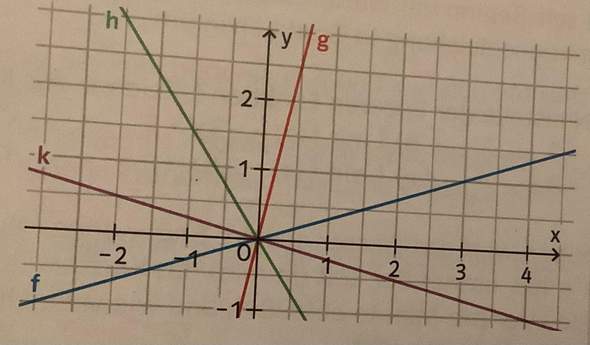
Wie in diesem Beispiel , Ich habe mithilfe einer Lösung herausgefunden, dass die Graphen , h, und , k, sinken und ,f, und ,g, steigen
ich habe aber trotzdem nicht verstanden warum der Graph ,g, steigt weil von dem Buchstaben ,g, aus sinkt der Graph doch
oder gibt es bestimmte Bereiche in einem Koordinaten System voran man erkennt ob ein Graph sinkt oder steigt , wie jetzt zum Beispiel die obere linke Seite ist für Graphen die sinken
3 Antworten
Geh mit dem Finger auf die Gerade, bewege den Finger auf der Geraden nach rechts.
Wandert dein Finger auf dem Weg nach rechts nach oben, ist die Steigung positiv.
Wandert dein Finger auf dem Weg nach rechts nach unten, ist die Steigung negativ.
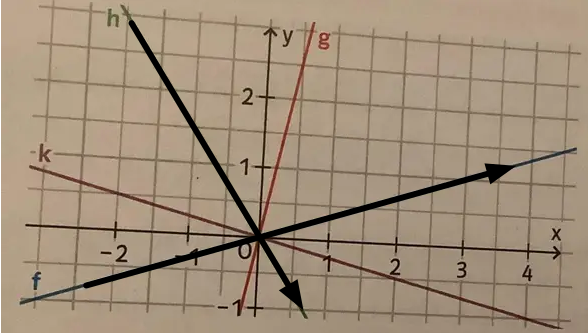
Von links unten nach rechts oben: positive Steigung.
Von links oben nach rechts unten: negative Steigung.
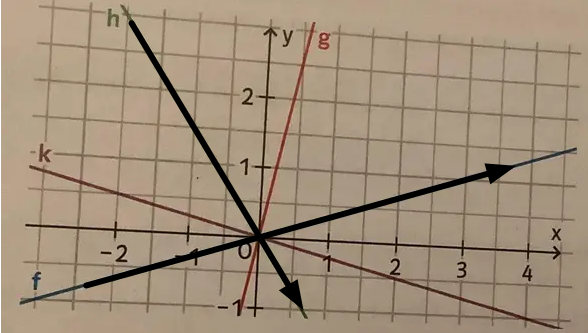
Die zu betrachtende Richtung ist immer die positive Richtung der x-Achse.
Stelle dir vor, dass du dich in Richtung der positiven x-Achse auf der jeweiligen Geraden bewegst.
Also zu den Graphen die in der x- Achsen Richtung laufen , steigen sie und die die in den y- Achsen laufen sinken :
die obere rechte Seite = positive - x- Achse = steigend
die linke obere Seite = negative -x- Achse = sinkend
Ich versuche noch eine andere Darstellung: Denke, dass du auf der x-Achse in positiver Richtung läufst und denke dir die Geraden als Straßen die du siehst. Dann kannst du dich fragen: Verläuft die Straße von unten nach oben oder von oben nach unten?
An den Vorzeichen von x und y
haben beide Werte das selbe Vorzeichen steigt der Graph
haben beide verschiedene Vorzeichen sinkt der Graph
WICHTIG:
Die Merkhilfe funktioniert nur, wenn der Graph durch (0l0) geht
Also wie in meinen Beispiel
der Graphen ,g, hat die Vorzeichen + , zum Beispiel g( 0,5/ 2,5 )
beide Punkte scheiden sich und haben beide das selbe Vorzeichen ( + ) , deswegen
Könnte ich bitte eine Erklärung bekommen , noch habe ich es nicht ganz verstanden