Woher leitet sich v=√{2·a·s} ab?
Woher leitet sich
ab?
Würde ich gerne mal wissen, es steht in meienr Formelsammlung ...
5 Antworten
Das ist die Engeschwindigkeit, wenn du pro Sekunde um a schneller wirst und mit 0 Geschwindigkeit startest und wenn du den Weg kennst, den du zurückgelegt hast.
Wovon leitet sich v=√{2·a·s} ab?
Die Formel habe ich zur Änderung vorgeschlagen, da 2·a·s komplett unter der Wurzel stehen sollen.
Es handelt sich um eine Formel, die für einen Spezialfall gilt, nämlich den einer gleichmäßigen Beschleunigung „aus dem Stand“, wobei Letzteres von der Wahl des Bezugssystems abhängt.
Das ist ein Koordinatensystem Σ, in dem man die Position
|r› = (x ¦ y ¦ z)
oder auch die Durchschnittsgeschwindigkeit
|v›.av = |Δr›/Δt
eines Körpers während der Zeitspanne zwischen t und t+Δt ausdrücken kann, die momentane Geschwindigkeit
.|v› = |dt›/dt = lim[Δt→0] |Δr›/Δt
oder auch die Beschleunigung
|a› = |dv›/dt = |d²r›/dt².
Es ist aber ebensogut möglich, ein anderes, gegenüber Σ beispielsweise gedrehtes Koordinatensystem Σ° oder ein relativ zu Σ bewengtes Koordinatensystem Σ′ als Bezugssystem zu verwenden, und dann wird aus „aus dem Stand“ eine Beschleunigung aus einer Bewegung heraus, vielleicht erst einmal in entgegengesetzter Richtung oder quer zur anfänglichen Bewegung.
In solchen Fällen gilt die Formel so nicht.
Sie gilt, wie gesagt, für eine gleichmäßige Beschleunigung „aus dem Stand“, wobei dann s die Länge des zurückgelegten Weges ist. Bei einer geradlinigen Bewegung ist das gleichbedeutend mit der Komponente der Position in Bewegungsrichtung. Desweiteren ist v entweder Betrag oder eine Komponente der Geschwindigkeit am Ende der Beschleunigungsphase, nämlich ebenfalls in Bewegungsrichtung, und a Entsprechendes für die Beschleunigung.
Alternativ dazu kann auch eine Abbremsung auf 0 gemeint sein. Dann allerdings ist v die Anfangsgeschwindigkeit.
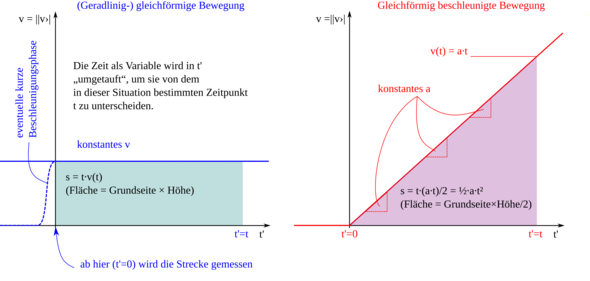
Für den ersten Fall habe ich ein Schaubild, ein t-v-Diagramm angefertigt. Es vereinigt a,v und s in einem Bild: a als Steigung der Geraden, v als Gerade selbst und s als Fläche unter der Geraden. Die bekanntere Formel
(1) s = ½at²
lässt sich so über die Formel von Dreiecksflächen berechnen. Außerdem ist
(2) s = ½v(t)·t,
wobei der Faktor ½ auftritt, weil die Durchschnittsgeschwindigkeit für die Zeitspanne [0, t] gerade ½v(t) ist. Um t, das vielleicht nicht gegeben ist, zu eliminieren, müssen wir die Gleichungen quadrieren und gleichsetzen und gleiches sofort wegkürzen:
(3) v(t)² = a²t² = a·at² = a·2s.
Auf dasselbe Ergebnis kommst Du auch, indem Du die kinetische Energie
E[kin](t) = ½mv(t)²
mit der Beschleunigungsarbeit
W = F·s(t) = m·a·s(t)
gleichsetzt. Die Masse m kürzt sich sofort raus, und da Du v haben willst, musst Du beide Seiten verdoppeln.
1) Definition der Beschleunigung:
a = dv/dt
dv = a ⋅ dt
2 ) Definition der Geschwindigkeit:
v = ds/dt
dt = ds/v
3) Einsetzen:
dv = a ⋅ ds / v
v ⋅ dv = a ⋅ ds
4) Beide Seiten integrieren und annehmen, dass
- a=const
- s(t=0) = 0
- v(t=0) = 0
½ v² = a ⋅ s
bzw.
v² = 2 ⋅ a ⋅ s
Aus der Höhenenergie m*g*h bzw. in deinem Fall m*a*s.
Diese stellt man mit der kinetischen Energie 1/2 * m * v² gleich, also:
m*a*s = 1/2 * m * v²
und löst nach v auf => v = Wurzel(2*a*s)
Anscheinend leitet sich deine allgemeine Formel doch eher von der gleichmäßig beschleunigten Bewegung ab mit:
s=1/2 * a * t² (1) und v= a*t (2) => (2) umstellen t =v/a
Führt in (1) eingesetzt zu:
s = 1/2 * a * v²/a² = 1/2 * v²/a
Und das nach v umgestellt eben zu deiner Formel.
Was genau soll unter der Wurzel stehen ? Verwende Klammern !!
Und nach welcher Variablen soll abgeleitet werden ?
Oder was genau willst du überhaupt erfahren ?
Wofür sollen v, a, s stehen ?
Alles soll unter der Wurzel stehen
v soll abgeleitet werden also die Geschwindigkeit warum sie sich bei der gleichmäßig beschleunigten Bewegung so berechnen lässt
a ist die Beschleunigung und s die Strecke die zurück gelegt wird.
Merci Beacoupe =)