Will mir jemand beim lösen einer Gleichung helfen?
Hallo ,ich bin gerade am Lernen und benötige Hilfe bei einer Aufgabe .Die Orange unterstrichene Aufgabe raubt mir die Zeit.Die Lösung besitze ich bereits doch ich komme nicht auf den Lösungsweg.Lösung : x=1 (minus 2 ist laut der Probe nicht eine Lösung)

Es ist bestimmt ganz einfach ,nur ich bin zu doof.Mich würde auch ein kleiner Tipp zufrieden stellen. LG der zukünftige Ingenieur
2 Antworten
Bevor Du quadrierst, notiere bitte x ≥ -3.
Genau hinsehen (oder pq-Formel verwenden):
Daher:
Satz von Nullprodukt:
Da das Quadrieren keine Äquivalenzumformung ist, musst Du zwingend prüfen, ob durch das Quadrieren eine neue Lösung erzeugt wurde (Probe) und dabei zeigt sich, dass x=-2 die Gleichung nicht löst. In diesem Zusammenhang steht auch mein erster Satz in dieser Antwort, auch wenn die weitere Rechnung zeigt, dass er keine Rolle spielt.
Skizze:

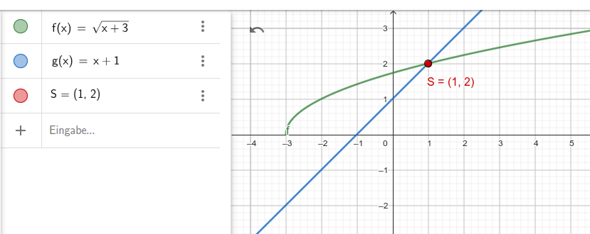
Ich erinnere: Die Wurzel einer Zahl x ist die positive Lösung der Gleichung y=x². Das ist schon alleine aus dem Wunsch, dass es eine Wurzelfunktion geben soll, eine zwingende Forderung.
Ich hoffe doch, wir bleiben bei der Wurzeldefinition für reelle Zahlen 😉.
-x und -3
0 = x² + x - 2
pq - Formel mit p = +1 und q = -2
.
Weil Wurzel in Ausgangsgleichung muss man die Lösungen noch testen
.
..
...
1*-2 = -2 = q
1 + -2 = -1 = -p
die Lösungen erfüllen die quadratische Glg
ABER -2 nicht
Wurzel(-2 + 3) = w(+1) = NUR + 1 , -1 nicht erlaubt , weil Wurzeln positiv sein müssen .
Daher -1 gleich -2+1 = -1 nicht möglich
weil es eine Quadratische Glg ist mit 1x² nimmt man die
Kannst auch ABC nehmen oder quadratische Ergänzung
Ich habe bisher nur qua Glg ausgeklammert und kaum Mitternachtsformel und Pq Formel verwendet.
ja , das geht hier nicht , wegen der Zahl -2 . Denn mit 0 = x*(x+1) -2 kommt man nicht weiter
also musst du ABC = Mitternacht oder pq verwenden
bzw quadratische Ergänzung . Was aber nix anderes als die Vorstufe zur pq ist
mit der Überraschung für mich , dass Wurzel(-2+3) = w(1) = -1 nicht zugelassen ist